��Ŀ����
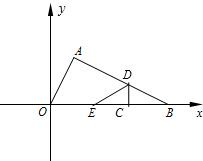
 ��ͼ��Rt��AOB�У���BAO=90�㣬OΪ����ԭ�㣬B��x���������ϣ�A�ڵ�һ���ޣ�OA��AB�ij��Ƿ���x2-3
��ͼ��Rt��AOB�У���BAO=90�㣬OΪ����ԭ�㣬B��x���������ϣ�A�ڵ�һ���ޣ�OA��AB�ij��Ƿ���x2-3| 5 |
��1����ֱ��AB�Ľ���ʽ��
��2������AOB�ش�ֱ��x����߶�CD�۵�����C��x���ϣ��Ҳ����B�غϣ���D���߶�AB�ϣ���ʹ��B����x���ϣ���Ӧ��ΪE���Ƿ���������ĵ�C��ʹ�á�AEDΪֱ�������Σ������ڣ������C�����ꣻ�������ڣ���˵�����ɣ�
��������1����OA��AB�ij��Ƿ���x2-3
+10=0����������OA��AB����˷��̼������OA��AB�ij���Ȼ���ɹ��ɶ������OB�ij��������õ�B�����ꣻȻ����AF��x����F����ֱ�������ε����ʣ��������AF�ij����̶��ɹ��ɶ������OF�ij����������A�����꣬Ȼ���ɴ���ϵ�������ֱ��AB�Ľ���ʽ��
��2���ֱ�Ӣ�����Rt��AED�Ե�AΪֱ�Ƕ���ʱ����E��ԭ��O�غ��뢢����Rt��AED�Ե�EΪֱ�Ƕ���ʱȥ������⼴����ô𰸣�
| 5 |
��2���ֱ�Ӣ�����Rt��AED�Ե�AΪֱ�Ƕ���ʱ����E��ԭ��O�غ��뢢����Rt��AED�Ե�EΪֱ�Ƕ���ʱȥ������⼴����ô𰸣�
����⣺��1����x2-3
+10=0��
����x-
����x-2
��=0��
��x1=
��x2=2
��
��OA��AB�ij��Ƿ���x2-3
+10=0����������OA��AB��
��OA=
��AB=2
��
�ߡ�BAO=90�㣬
��OB=
=5��
��AF��x����F����ͼ�٣�
��AF=
=
=2��
��OF=
=
=1��
��A��1��2����B��5��0����
��ֱ��AB�Ľ���ʽΪy=kx+b��
����
��
���
��
��ֱ��AB�Ľ���ʽΪ��y=-
x+
��
��2�����ڣ�
������������ۣ�
������Rt��AED�Ե�AΪֱ�Ƕ���ʱ����E��ԭ��O�غϣ���ͼ�ڣ�
��OC=BC=
OB=
��
��C1��
��0����
������Rt��AED�Ե�EΪֱ�Ƕ���ʱ����ͼ�ۣ�����A��AF��x����F��
��OF=1��
�ߡ�AED=90�㣬
���AEO+��DEC=90�㣮
�ߡ�DEC=��DBC��
���AEO+��DBC=90�㣮
�֡ߡ�AOE+��DBC=90�㣬
���AOE=��AEO��
���AOE�ǵ��������Σ�
��OE=2OF=2��
��BE=3��
��EC=
��
��OC=OE+EC=2+
=
��
��C2��
��0����
�������������������ĵ�C��ʹ�á�AEDΪֱ�������Σ���C������Ϊ��C1��
��0����C2��
��0����
| 5 |
����x-
| 5 |
| 5 |
��x1=
| 5 |
| 5 |
��OA��AB�ij��Ƿ���x2-3
| 5 |
��OA=
| 5 |
| 5 |
�ߡ�BAO=90�㣬
��OB=
(
|
��AF��x����F����ͼ�٣�
��AF=
| OA•AB |
| OB |
| ||||
| 5 |
��OF=
| OA2-AF2 |
(
|
��A��1��2����B��5��0����

��ֱ��AB�Ľ���ʽΪy=kx+b��
����
|
���
|
��ֱ��AB�Ľ���ʽΪ��y=-
| 1 |
| 2 |
| 5 |
| 2 |
��2�����ڣ�
������������ۣ�
������Rt��AED�Ե�AΪֱ�Ƕ���ʱ����E��ԭ��O�غϣ���ͼ�ڣ�
��OC=BC=
| 1 |
| 2 |
| 5 |
| 2 |
��C1��
| 5 |
| 2 |
������Rt��AED�Ե�EΪֱ�Ƕ���ʱ����ͼ�ۣ�����A��AF��x����F��
��OF=1��
�ߡ�AED=90�㣬
���AEO+��DEC=90�㣮
�ߡ�DEC=��DBC��
���AEO+��DBC=90�㣮
�֡ߡ�AOE+��DBC=90�㣬
���AOE=��AEO��
���AOE�ǵ��������Σ�
��OE=2OF=2��
��BE=3��
��EC=
| 3 |
| 2 |
��OC=OE+EC=2+
| 3 |
| 2 |
| 7 |
| 2 |
��C2��
| 7 |
| 2 |
�������������������ĵ�C��ʹ�á�AEDΪֱ�������Σ���C������Ϊ��C1��
| 3 |
| 2 |
| 7 |
| 2 |
���������⿼���˴���ϵ������һ�κ����Ľ���ʽ��ֱ�������ε����ʡ����������ε��ж��������Լ�һԪ���η��̵Ľⷨ�������ѶȽϴ�ע�����շ���˼�롢��������˼�������ν��˼���Ӧ�ã�

��ϰ��ϵ�д�
 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�
�����Ŀ
 ��ͼ��Rt��AOB�У���BAO=90�㣬OΪ����ԭ�㣬B��x���������ϣ�A�ڵ�һ���ޣ�OA��AB�ij��Ƿ���
��ͼ��Rt��AOB�У���BAO=90�㣬OΪ����ԭ�㣬B��x���������ϣ�A�ڵ�һ���ޣ�OA��AB�ij��Ƿ���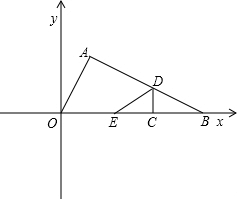 ��ͼ��Rt��AOB�У���BAO=90�㣬OΪ����ԭ�㣬B��x���������ϣ�A�ڵ�һ���ޣ�OA��AB�ij��Ƿ���
��ͼ��Rt��AOB�У���BAO=90�㣬OΪ����ԭ�㣬B��x���������ϣ�A�ڵ�һ���ޣ�OA��AB�ij��Ƿ���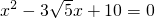 ��������OA��AB��
��������OA��AB�� ��������OA��AB��
��������OA��AB��
