题目内容
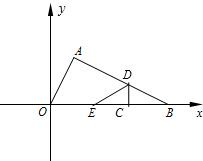 如图在Rt△AOB中,∠BAO=90°,O为坐标原点,B在x轴正半轴上,A在第一象限.OA和AB的长是方程x2-3
如图在Rt△AOB中,∠BAO=90°,O为坐标原点,B在x轴正半轴上,A在第一象限.OA和AB的长是方程x2-3| 5 |
(1)求直线AB的解析式;
(2)将△AOB沿垂直于x轴的线段CD折叠(点C在x轴上,且不与点B重合,点D在线段AB上),使点B落在x轴上,对应点为E,设点C的坐标为(x,0).
①是否存在这样的点C,使得△AED为直角三角形?若存在,求出点C的坐标;若不存在,请说明理由;
②设△CDE与△AOB重叠部分的面积为S,直接写出S与点C的横坐标x之间的函数关系式(包括自变量x的取值范围).
分析:(1)根据题意可直接求出OA、AB的长,又∠BAO=90°,由勾股定理可求OB,作OB边上的高AF,用面积法及勾股定理可求0F、AF,从而得出A点坐标,根据“两点法”求直线AB解析式.
(2)△AED按直角顶点分为两类:①A点为直角顶点,此时E、O两点重合,C点为OB的中点;②E点为直角顶点,过点A作AF⊥x轴于F,利用等腰三角形的性质解题.
(2)△AED按直角顶点分为两类:①A点为直角顶点,此时E、O两点重合,C点为OB的中点;②E点为直角顶点,过点A作AF⊥x轴于F,利用等腰三角形的性质解题.
解答: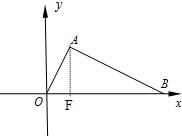 解:(1)解方程x2-3
解:(1)解方程x2-3
x+10=0得两根为x1=
,x2=2
因为OA和AB的长是方程x2-3
x+10=0两根,且OA<AB
所以OA=
,AB=2
而∠BAO=90°,则OB=
=5
作AF⊥x轴于F,如图
则AF=
=
=2
那么OF=
=1
∴A(1,2),B(5,0).
设直线AB的解析式为y=kx+b,则有
,
解得
.
∴直线AB的解析式为y=-
x+
.
(2)①存在.
分两种情况讨论:
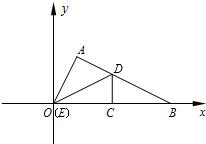
ⅰ)当Rt△AED以点A为直角顶点时,点E与原点O重合,如图.
∵OC=BC=
OB=
∴C1(
,0);
ⅱ)当Rt△AED以点E为直角顶点时,如图,过点A作AF⊥x轴于F.OF=1.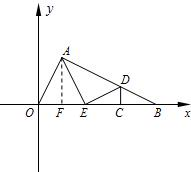
∵∠AED=90°,
∴∠AEO+∠DEC=90°.
∵∠DEC=∠DBC,
∴∠AEO+∠DBC=90°.
又∵∠AOE+∠DBC=90°,
∴∠AOE=∠AEO.
∴△AOE是等腰三角形,
∴OE=2OF=2,
∴BE=3.
∴EC=
,
∴OC=OE+EC=2+
=
.
∴C2(
,0).
综上所述,存在这样的点C,使得△AED为直角三角形,点C的坐标为:
C1(
,0)和C2(
,0).
②当1≤x<
时,△CDE与△AOB重叠部分的面积即为△CDE的面积,由直角三角形的面积公式即可求解;
S与x之间的函数关系式如下:
S=
.
 解:(1)解方程x2-3
解:(1)解方程x2-3| 5 |
| 5 |
| 5 |
因为OA和AB的长是方程x2-3
| 5 |
所以OA=
| 5 |
| 5 |
而∠BAO=90°,则OB=
(
|
作AF⊥x轴于F,如图
则AF=
| OA•AB |
| OB |
| ||||
| 5 |
那么OF=
(
|
∴A(1,2),B(5,0).
设直线AB的解析式为y=kx+b,则有
|

解得
|
∴直线AB的解析式为y=-
| 1 |
| 2 |
| 5 |
| 2 |
(2)①存在.
分两种情况讨论:
ⅰ)当Rt△AED以点A为直角顶点时,点E与原点O重合,如图.
∵OC=BC=
| 1 |
| 2 |
| 5 |
| 2 |
∴C1(
| 5 |
| 2 |
ⅱ)当Rt△AED以点E为直角顶点时,如图,过点A作AF⊥x轴于F.OF=1.

∵∠AED=90°,
∴∠AEO+∠DEC=90°.
∵∠DEC=∠DBC,
∴∠AEO+∠DBC=90°.
又∵∠AOE+∠DBC=90°,
∴∠AOE=∠AEO.
∴△AOE是等腰三角形,
∴OE=2OF=2,
∴BE=3.
∴EC=
| 3 |
| 2 |
∴OC=OE+EC=2+
| 3 |
| 2 |
| 7 |
| 2 |
∴C2(
| 7 |
| 2 |
综上所述,存在这样的点C,使得△AED为直角三角形,点C的坐标为:
C1(
| 5 |
| 2 |
| 7 |
| 2 |
②当1≤x<
| 5 |
| 2 |
S与x之间的函数关系式如下:
S=
|
点评:本题考查了点的坐标的求法,待定系数法求直线解析式,折叠问题及分类讨论的数学思想.

练习册系列答案
相关题目
 如图在Rt△AOB中,∠BAO=90°,O为坐标原点,B在x轴正半轴上,A在第一象限,OA和AB的长是方程
如图在Rt△AOB中,∠BAO=90°,O为坐标原点,B在x轴正半轴上,A在第一象限,OA和AB的长是方程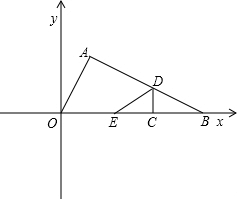 如图在Rt△AOB中,∠BAO=90°,O为坐标原点,B在x轴正半轴上,A在第一象限,OA和AB的长是方程
如图在Rt△AOB中,∠BAO=90°,O为坐标原点,B在x轴正半轴上,A在第一象限,OA和AB的长是方程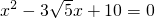 两根,且OA<AB.
两根,且OA<AB. 两根,且OA<AB.
两根,且OA<AB.
