题目内容
【题目】在△ABC中,a,b,c分别为∠A,∠B,∠C所对的边,我们称关于x的一元二次方程![]() 为“△ABC的☆方程”.根据规定解答下列问题:
为“△ABC的☆方程”.根据规定解答下列问题:
(1)“△ABC的☆方程” ![]() 的根的情况是______(填序号):
的根的情况是______(填序号):
①有两个相等的实数根;②有两个不相等的实数根;③没有实数根;
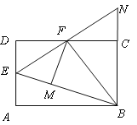
(2)如图,AD为⊙O的直径,BC为弦, BC⊥AD于E,∠DBC=30°,求“△ABC的☆方程” ![]() 的解;
的解;

(3)若x=![]() 是“△ABC的☆方程”
是“△ABC的☆方程” ![]() 的一个根,其中a,b,c均为整数,且
的一个根,其中a,b,c均为整数,且![]() ,求方程的另一个根.
,求方程的另一个根.
【答案】(1)选②(2)![]() (3)x1=
(3)x1=![]() ,x2=-2.
,x2=-2.
【解析】
试题分析:(1)利用三角形各边大于0,再利用![]() ,得出答案即可;
,得出答案即可;
(2)利用等边三角形的判定得出△ABC为等边三角形,进而得出a=b=c,求出方程的根即可;
(3)将![]() 代入☆方程可得:
代入☆方程可得:![]() ,进而化简得出
,进而化简得出![]() ,结合
,结合![]() ,可得
,可得![]() ,进而求出a,b,c的值求出方程的根即可.
,进而求出a,b,c的值求出方程的根即可.
试题解析:(1)选②
(2)由角度推导出△ABC为等边三角形,等a=b=c
△ABC的☆方程”ax2+bx-c=0可以变为:ax2+ax-a=0,
∵a≠0,方程进一步化简为:x2+x-1=0解之得:![]()
(3)将x=![]() 代入☆方程中可得:
代入☆方程中可得:![]() 化简可得:ac+4b-16=0,
化简可得:ac+4b-16=0,
结合ac-4b<0,可得出0<ac<8,
由ac+4b=16,可知ac需能被4整除,又0<ac<8;
∴ac=4,从而b=3,
又因为a,c为正整数,则a=1,c=4(不能构成三角形,舍去)或者a=c=2,
所以☆方程为2x2+3x-2=0,![]() 解得:x1=
解得:x1=![]() ,x2=-2.
,x2=-2.

练习册系列答案
相关题目