题目内容
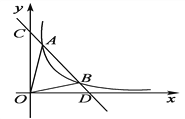
【题目】如图,过点C(1,2)分别作x轴,y轴的平行线,交直线y=-x+6于点A,B,若反比例函数y=![]() (x>0)的图象与△ABC有公共点,求k的取值范围.
(x>0)的图象与△ABC有公共点,求k的取值范围.

【答案】2≤k≤9
【解析】先求出点A、B的坐标,根据反比例函数系数的几何意义可知,当反比例函数图象与△ABC相交于点C时k的取值最小,当与线段AB相交时,k能取到最大值,根据直线y=-x+6,设交点为(x,-x+6)时k值最大,然后列式利用二次函数的最值问题解答即可得解.
∵点C(1,2),BC∥y轴,AC∥x轴,
∴当x=1时,y=-1+6=5,
当y=2时,-x+6=2,解得x=4,
∴点A、B的坐标分别为A(4,2),B(1,5),
根据反比例函数系数的几何意义,当反比例函数与点C相交时,k=1×2=2最小,
设反比例函数与线段AB相交于点(x,-x+6)时k值最大,
则k=x(-x+6)=-x2+6x=-(x-3)2+9,
∵1≤x≤4,
∴当x=3时,k值最大,
此时交点坐标为(3,3),
因此,k的取值范围是2≤k≤9.

练习册系列答案
相关题目