题目内容
【题目】当m为何值时，关于x的一元二次方程（2m+1）x2+4mx+2m﹣3=0．
（1）有两个不相等的实数根；
（2）有两个相等的实数根；
（3）没有实数根．
【答案】
（1）解：（2m+1）x2+4mx+2m﹣3=0，
△=（4m）2﹣4（2m+1）（2m﹣3）=16m+12，
2m+1≠0时，m≠﹣ 
当△＞0时，有两个不相等的实数根，即当m＞﹣ 
且m≠﹣ 时，方程有两个不相等的实数根
（2）解：当△=0时，有两个不相等的实数根，即当m=﹣ 时，方程有两个相等的实数根
（3）解：当△＜0时，没有实数根，即当m＜﹣ 时，方程没有实数根
【解析】先求出△的值，再根据根的判别式的内容判断即可．
【考点精析】掌握求根公式是解答本题的根本，需要知道根的判别式△=b2-4ac，这里可以分为3种情况：1、当△>0时，一元二次方程有2个不相等的实数根2、当△=0时，一元二次方程有2个相同的实数根3、当△<0时，一元二次方程没有实数根．
练习册系列答案
津桥教育计算小状元系列答案
相关题目
【题目】一位射击运动员在10次射击训练中，命中靶的环数如图． 请你根据图表，完成下列问题：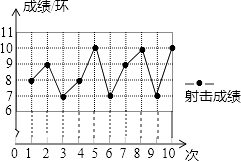
（1）补充完成下面成绩表单的填写：
射击序次 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
成绩/环 | 8 | 10 | 7 | 9 | 10 | 7 | 10 |
（2）求该运动员这10次射击训练的平均成绩．
