Question

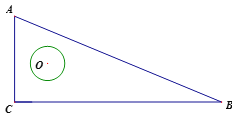
【题目】如图，在△ABC中，AC：BC：AB=5：12：13,⊙O在△ABC内自由移动，若⊙O的半径为1，且圆心O在△ABC内所能到达的区域的面积为，则△ABC的周长为______.

Answer 1

【答案】25

【解析】

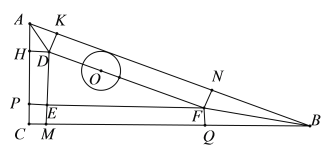
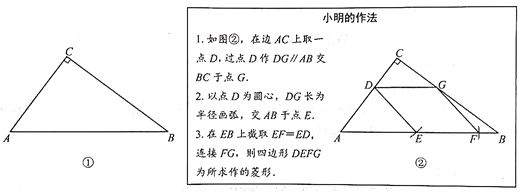
如图，可知圆心O在△ABC内所能到达的区域为△DEF的边以及其内部，其中点D在∠BAC的角平分线上，且到AB、AC边的距离为1，点E在∠ACB的角平分线上，且到CA、CB边的距离为1，点F在∠ABC的角平分线上，且到BA、BC边的距离为1，DH、EP分别垂直于AC，EM、FQ分别垂直于BC，DK、FN分别垂直于AB，

则有AH=AK，CP=CM=EM=1，BN=BQ，四边形EDPH、EFQM、DFNK是矩形，△DEF是直角三角形且△DEF∽△ACB，继而根据已知可分别求出DE、EF、DF的长，再设AH=AK=x，BN=BQ=y，

则有AC =x+，BC=5+y，AB= x+y+，再根据AC：BC：AB=5：12：13列方程组可求出x、y的值，继而根据三角形的周长公式进行求解即可.

如图，可知圆心O在△ABC内所能到达的区域为△DEF的边以及其内部，其中点D在∠BAC的角平分线上，且到AB、AC边的距离为1，点E在∠ACB的角平分线上，且到CA、CB边的距离为1，点F在∠ABC的角平分线上，且到BA、BC边的距离为1，DH、EP分别垂直于AC，EM、FQ分别垂直于BC，DK、FN分别垂直于AB，

则有AH=AK，CP=CM=EM=1，BN=BQ，四边形EDPH、EFQM、DFNK是矩形，△DEF是直角三角形且△DEF∽△ACB，

又∵AC：BC：AB=5：12：13，

∴DE：EF：DF=5：12：13，

又∵S△DEF=DEEF=，

∴DE=，EF=4，

∴DF=，

∴PH=DE=，MQ=EF=4，NK=DF=，

设AH=AK=x，BN=BQ=y，

则有AC=AH+HP+CP=x+，BC=CM+MQ+BQ=5+y，AB=AK+NK+BN=x+y+，

又∵AC：BC：AB=5：12：13，

∴，

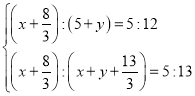解得：，

∴AC=+，BC=10，AB=++5，

∴AC+BC+AB=++10+++5=7+3+10+5=25，

故答案为：25.