题目内容
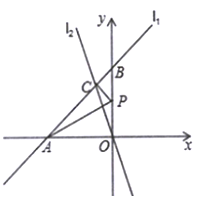
【题目】已知,如图,在平面直角坐标系![]() 中,直线
中,直线![]() 分别交
分别交![]() 轴、
轴、![]() 轴于点
轴于点![]() 、
、![]() 两点,直线
两点,直线![]() 过原点且与直线
过原点且与直线![]() 相交于
相交于![]() ,点
,点![]() 为
为![]() 轴上一动点.
轴上一动点.
(1)求点![]() 的坐标;
的坐标;
(2)求出![]() 的面积;
的面积;
(3)当![]() 的值最小时,求此时点
的值最小时,求此时点![]() 的坐标;
的坐标;
【答案】(1)点![]() ;(2)
;(2)![]() ;(3)点
;(3)点![]() .
.
【解析】
(1)联立两直线解析式组成方程组,解得即可得出结论;
(2)将![]() 代入
代入![]() ,求出OB的长,再利用 (1)中的结论点
,求出OB的长,再利用 (1)中的结论点![]() ,即可求出
,即可求出![]() 的面积;
的面积;
(3)先确定出点A关于y轴的对称点A',即可求出PA+PC的最小值,再用待定系数法求出直线A'C的解析式即可得出点P坐标.
解:(1)∵直线l1:y=x+3与直线l2:y=-3x相交于C,
∴![]()
解得: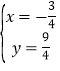
∴点![]() ;
;
(2) ∵把![]() 代入
代入![]() ,
,
解得:![]() ,
,
∴![]() ,
,
又∵点![]() ,
,
∴![]()
![]()
![]() ;
;
(3) 如图,作点A(-3,0)关于y轴的对称点A'(3,0),
连接CA'交y轴于点P,此时,PC+PA最小,
最小值为CA'=![]() ,
,
由(1)知,![]() ,
,
∵A'(3,0),
∴直线A'C的解析式为![]() ,
,
∴点![]() .
.

练习册系列答案
 英才计划期末调研系列答案
英才计划期末调研系列答案
相关题目