题目内容
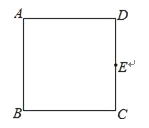
【题目】己知图甲是一个长为2m、宽为2n的长方形，沿图甲中虚线用剪刀均匀分成四小块长方形，然后按图乙的形状拼成一个正方形．
（1)图乙中阴影部分正方形的边长为________（用含字母m，n的整式表示）．
（2）请用两种不同的方法求图乙中阴影部分的面积．
方法一：________________；
方法二：________________．
【答案】（1）m-n；（2）（m+n）2-4mn，（m-n）2
【解析】
平均分成后，每个小长方形的长为m，宽为n．
（1）正方形的边长=小长方形的长-宽；
（2）第一种方法为：大正方形面积-4个小长方形面积；第二种表示方法为：阴影部分为小正方形的面积.
解：（1）图乙中阴影部分正方形的边长为m-n；
（2）方法一：大正方形面积-4个小长方形面积=（m+n）2-4mn；
方法二：阴影部分为小正方形的面积=（m-n）2；
故答案为：（1）m-n；（2）（m+n）2-4mn，（m-n）2
练习册系列答案
相关题目
【题目】某次数学单元测试，七年级第一小组共10名同学，小组长把超过班级平均分的部分记为“＋”，不足的部分记为“－”，记录如表：
与平均分的差值（分) | －15 | －9 | 0 | ＋3 | ＋12 | ＋17 |
人数 | 1 | 2 | 1 | 2 | 3 | 1 |
根据表格数据解答下列问题：
（1）第一小组同学的平均分比班级平均分高还是低?高或低多少分?
（2）若该班这次测试的平均分为80分，求第一小组10名同学的总分．
