题目内容
【题目】为了了解某校九年级学生的跳高水平，随机抽取该年级50名学生进行跳高测试，并把测试成绩绘制成如图所示的频数表和未完成的频数直方图（每组含前一个边界值，不含后一个边界值）．
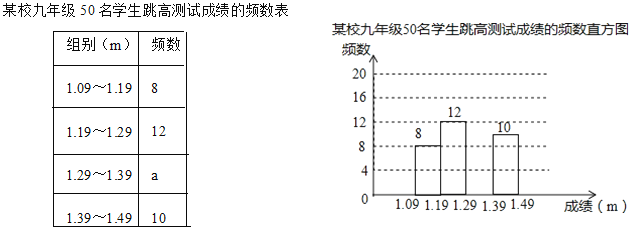
（1）求a的值，并把频数直方图补充完整；
（2）该年级共有500名学生，估计该年级学生跳高成绩在1.29m（含1.29m）以上的人数．
【答案】（1）a=20，补图见解析；（2）300人
【解析】
（1）利用总人数减去各个组别的人数即可求出a的值，然后补全频数直方图即可；
（2）利用500乘跳高成绩在1.29m（含1.29m）以上的人数的频率即可得出结论．
解：（1）a=50-8-12-10=20，
；
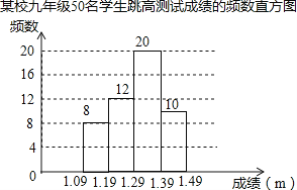（2）该年级学生跳高成绩在1.29m（含1.29m）以上的人数是：500×
=300（人）
答：该年级学生跳高成绩在1.29m（含1.29m）以上有300人．
黄冈小状元口算速算练习册系列答案
成功训练计划系列答案
倍速训练法直通中考考点系列答案
一卷搞定系列答案
名校作业本系列答案【题目】已知二次函数
．
（1）该二次函数的顶点坐标为__________；
（2）该函数的图象与
轴的交点坐标为__________；
（3）用五点法画函数图象
| … | … | |||||
| … | … |
（4）当
时，则
的取值范围是__________；
（5）将该抛物线绕顶点旋转180°，所得函数的解析式为__________；
（6）抛物线
与轴有且仅有一个交点，则
__________．
【题目】为了解某校七年级学生作业时间情况，随机抽取了该校七年级部分学生进行调查，并根据调查结果绘制了如下的统计图．
作业时间分组表（单位：小时）
别 | 作业时间 | 人数 | 频率 |
A | 1≤x≤1.5 | 5 | 0.1 |
B | 1.5≤x≤2 | 20 | b |
C | 2≤x≤2.5 | m | n |
D | x≥2.5 | 7 | 0.14 |
小计 | a | 1 |
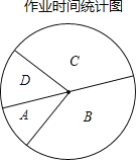
（1）统计图中的a=______；b=______；m=______；n=______．
（2）求出C组的扇形的圆心角度数．
（3）如果该校七年级学生共400名，试估计这400名生作业时间在B组和C组的人数共有多少人？