��Ŀ����
����Ŀ������ʶ���
��P��Q�ֱ�������ͼ��G1��G2�ϵ�����һ�㣬��P��Q����֮��ľ�����Сʱ�����ǰ������С�������ͼ��G1��G2�����ܾ��룬��Ϊd(G1��G2)�����磬�����M��N�ֱ��������ֱཻ��a��b�ϵ�����һ�㣬��d(a��b)��0
���������ã�
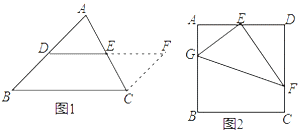
��ͼ1���������ĸ�����ֱ��ǵ�A��B��C��D����AB��CD��5��AD��BC��3����ôd(AB��CD)��___��d(AD��BC)��_____��d(AD��AB)��_____��
������̽����
(1)��ͼ1�У�������߶�CD��������ֱ��ƽ��(��AB����)����ʹd(CD��AB)���䣬��ô�߶�CD���е�ƫ����ԭ��λ�õ�������Ϊ______��
(2)��ͼ2���߶�AB��ֱ��CD��AB��1����A��CD�ľ���Ϊ3�����߶�AB�Ƶ�A��ת90����Ķ�Ӧ�߶�ΪAB������d(AB����CD)��______��

���𰸡����������á�d��AB��CD����3��d��AD��BC����5��d��AD��AB����0��������̽������1��CD��ԭ�е�E��ƽ�ƺ���е�F��������Ϊ��5����2��d��AB�䣬CD����2��3��
��������
[��������]����ͼ��G1��G2�����ܾ���Ķ���ɵý��ۣ�
[����̽��]��1����ͼ1�У�ע���߶�CDƽ�Ƶ���Զ���룬�ɵý��ۣ�
��2����ͼ2��Ҫ��������ۣ�����˳ʱ�����ʱ����ת���������ܾ���Ķ��������⣮
�⣺[��������]
��ͼ1����AB��CD�ľ���ΪAD��3��
��d��AB��CD����3��
��AD��BC�ľ���Ϊ5��
��d��AD��BC����5��
��AD��AB���ڵ�B��
��d��AD��AB����0��
[����̽��]
��1����ͼ��ʾ��
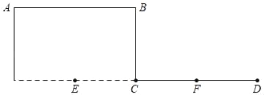
CD��ԭ�е�E��ƽ�ƺ���е�F��������Ϊ��5��
��2�����߶�AB�Ƶ�A��ת90���Ķ�Ӧ�߶�ΪAB���AB'����ͼ2���ӳ�AB'��CD��E��
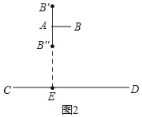
��AB��AB'��AB'��1��
��AE��3��
��B'E��2��
��d��AB�䣬CD����2��3��

 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�