Question

【题目】(1)方法回顾

在学习三角形中位线时，为了探索三角形中位线的性质，思路如下：

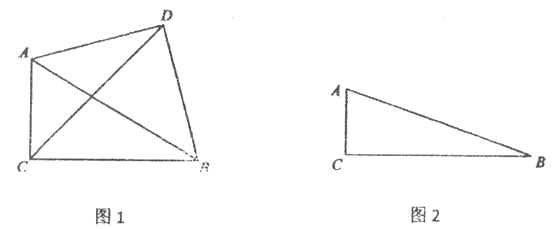
第一步添加辅助线：如图1，在△ABC中，延长DE (D、E分别是AB、AC的中点)到点F，使得EF＝DE，连接CF；

第二步证明△ADE≌△CFE，再证四边形DBCF是平行四边形，从而得到DE∥BC，DE＝BC．

(2)问题解决

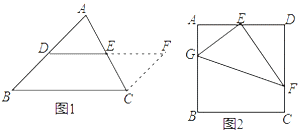
如图2，在正方形ABCD中，E为AD的中点，G、F分别为AB、CD边上的点，若AG＝2，DF＝3，∠GEF＝90°，求GF的长．

(3)拓展研究

如图3，在四边形ABCD中，∠A＝100°，∠D＝110°，E为AD的中点，G、F分别为AB、CD边上的点，若AG＝4，DF＝，∠GEF＝90°，求GF的长．

Answer 1

【答案】问题解决：GF=5；拓展研究：GF=.

【解析】

（1）延长GE、FD交于点H，可证得△AEG≌△DEH，结合条件可证明EF垂直平分GH，可得GF=FH，可求得GF的长；

（2）过点D作AB的平行线交GE的延长线于点H，过H作CD的垂线，垂足为P，连接HF，可证明△AEG≌△DEH，结合条件可得到△HPD为等腰直角三角形，可求得PF的长，在Rt△HFP中，可求得HF，则可求得GF的长．

(1)如图2，延长GE、FD交于点H，

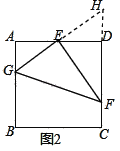
∵E为AD中点，

∴EA＝ED，且∠A＝∠EDH＝90°，

在△AEG和△DEH中，

∴△AEG≌△DEH(ASA)，

∴AG＝HD＝2，EG＝EH，

∵∠GEF＝90°，

∴EF垂直平分GH，

∴GF＝HF＝DH+DF＝2+3＝5；

(2)如图3，过点D作AB的平行线交GE的延长线于点H，过H作CD的垂线，垂足为P，连接HF，

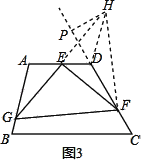
同(1)可知△AEG≌△DEH，GF＝HF，

∴∠A＝∠HDE＝100°，AG＝HD＝4，

∵∠ADC＝110°，

∴∠HDF＝360°﹣100°﹣110°＝150°，

∴∠HDP＝30°，∴HP＝2，

PD＝PH＝，

∴PF＝PD+DF＝

在Rt△HFP中，∠HPF＝90°，HP＝2，PF＝，

∴HF＝＝，

∴GF＝．