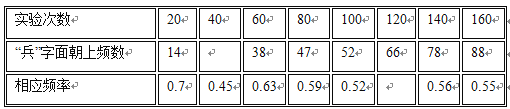
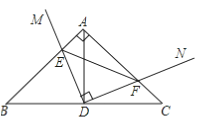
题目内容
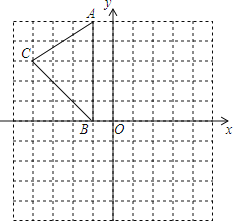
【题目】抛物线![]() 与
与![]() 轴交于点A,点B(1,0),与
轴交于点A,点B(1,0),与![]() 轴交于点C(0,﹣3),点M是其顶点.
轴交于点C(0,﹣3),点M是其顶点.
(1)求抛物线解析式;
(2)第一象限抛物线上有一点D,满足∠DAB=45°,求点D的坐标;
(3)直线![]() (﹣3<
(﹣3<![]() <﹣1)与x轴相交于点H.与线段AC,AM和抛物线分别相交于点E,F,P.证明线段HE,EF,FP总能组成等腰三角形.
<﹣1)与x轴相交于点H.与线段AC,AM和抛物线分别相交于点E,F,P.证明线段HE,EF,FP总能组成等腰三角形.
【答案】(1)![]() ;(2)(2,5);(3)答案见解析
;(2)(2,5);(3)答案见解析
【解析】试题分析:(1)把B、C的坐标代入,解方程组即可得到结论;
(2)令y=0,求出A、B的坐标,设直线AD交y轴于点N,求出求直线AN的解析式, 与抛物线联立成方程组,解方程组,即可得到D的坐标;
(3)求出直线AM、AC的解析式,当x=t时,表示出HE,HF,HP,得到HE=EF=HF﹣HE=t+3,FP=![]() ,由HE+EF﹣FP=
,由HE+EF﹣FP=![]() >0, 得到HE+EF>FP,再由HE+FP>EF,EF+FP>HE,得到当﹣3<t<﹣1时,线段HE,EF,FP总能组成等腰三角形.
>0, 得到HE+EF>FP,再由HE+FP>EF,EF+FP>HE,得到当﹣3<t<﹣1时,线段HE,EF,FP总能组成等腰三角形.
试题解析:解:(1)∵抛物线经过点B、C,∴ ![]() ,解得:
,解得: ![]() ,∴抛物线的解析式为:
,∴抛物线的解析式为: ![]() ;
;
(2)令y=0,得: ![]() ,解得:
,解得: ![]() ,
, ![]() ,∴A(﹣3,0),B(1,0),
,∴A(﹣3,0),B(1,0),
设直线AD交y轴于点N,∵∠DAB=45°,∴△NAO是等腰直角三角形,N(0,3),
可求直线AN的解析式为y=x+3,
联立![]() ,解得:
,解得: ![]() 或
或![]() ,∴D的坐标为(2,5);
,∴D的坐标为(2,5);
(3)M(﹣1,﹣4),
可求直线AM的解析式为:y=﹣2x﹣6,直线AC的解析式为y=﹣x﹣3,
∵当x=t时,HE=﹣(﹣t﹣3)=t+3,HF=﹣(﹣2t﹣6)=2t+6,HP=﹣(![]() )
)
∴HE=EF=HF﹣HE=t+3,FP=![]() ,
,
∵HE+EF﹣FP=![]() >0,
>0,
∴HE+EF>FP,又HE+FP>EF,EF+FP>HE,
∴当﹣3<t<﹣1时,线段HE,EF,FP总能组成等腰三角形.

 阅读快车系列答案
阅读快车系列答案