Question

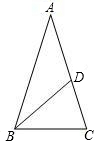
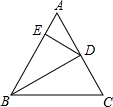
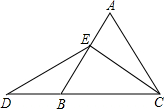
在等边△ABC中，点E在线段AB上，点D在CB的延长线上，且ED=EC．
（1）当点E为线段AB的中点时，试求

AE 4DB

的值；
（2）当点E不是线段AB的中点时，

AE 4DB

的值是否发生变化？为什么？

Answer 1

（1）过点E作EF⊥BC于F，设等边三角形的边长为2a，
∵点E为线段AB的中点，
∴AE=BE=

1

2

×2a=a，∠BCE=30°，
∵ED=EC，
∴∠D=∠BCE=30°，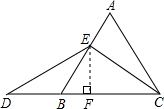
∴∠BED=∠ABC-∠D=60°-30°=30°，
∴BD=BE=a，

AE 4DB

=

a 4a

=

1

2

；

（2）不变．理由如下：
过点E作EF⊥BC于F，设BD=x，等边三角形的边长为2a，
∵ED=EC，
∴CF=

1

2

CD=

1

2

（2a+x），
∴BF=BC-CF=2a-

1

2

（2a+x）=a-

1

2

x，
在Rt△BEF中，BE=2BF=2a-x，
∴AE=AB-BE=2a-（2a-x）=x，
∴

AE 4DB

=

x 4x

=

1

2

．