题目内容
如图,在平面直角坐标系xOy中,一次函数y=ax+b的图象与反比例函数 的图象相交于点A(m,1)、B(﹣1,n),与x轴相交于点C(2,0),且AC=
的图象相交于点A(m,1)、B(﹣1,n),与x轴相交于点C(2,0),且AC= OC.
OC.
(1)求该反比例函数和一次函数的解析式;
(2)直接写出不等式ax+b≥ 的解集.
的解集.
解:(1)过A作AD⊥x轴,可得AD=1,
∵C(2,0),即OC=2,∴AC= OC=
OC= 。
。
在Rt△ACD中,根据勾股定理得:CD=1。
∴OD=OC+CD=2+1=3。∴A(3,1)。
将A、C的坐标代入一次函数解析式得: ,解得:
,解得: 。
。
∴一次函数解析式为y=x﹣2。
将A(3,1)代入反比例解析式得:k=3,
∴反比例解析式为 。
。
(2)根据图形得:不等式ax+b≥ 的解集为﹣1≤x<0或x≥3。
的解集为﹣1≤x<0或x≥3。
解析试题分析:(1)过A作AD垂直于x轴,如图所示,由C的坐标求出OC的长,根据AC= OC求出AC的长,由A的纵坐标为1,得到AD=1,利用勾股定理求出CD的长,有OC+CD求出OD的长,确定出m的值,将A于与C坐标代入一次函数解析式求出a于b的值,即可得出一次函数解析式;将A坐标代入反比例函数解析式求出k的值,即可确定出反比例解析式。
OC求出AC的长,由A的纵坐标为1,得到AD=1,利用勾股定理求出CD的长,有OC+CD求出OD的长,确定出m的值,将A于与C坐标代入一次函数解析式求出a于b的值,即可得出一次函数解析式;将A坐标代入反比例函数解析式求出k的值,即可确定出反比例解析式。
(2)将B坐标代入反比例解析式中求出n的值,确定出B坐标,利用图形即可得出所求不等式的解集:
将B(﹣1,n)代入反比例解析式得:n=﹣3,即B(﹣1,﹣3)。
根据图形得:不等式ax+b≥ 的解集为﹣1≤x<0或x≥3。
的解集为﹣1≤x<0或x≥3。

练习册系列答案
相关题目
 的图象与y轴交于点A,一次函数
的图象与y轴交于点A,一次函数 的图象 经过点B(0,-1),并且与x轴以及
的图象 经过点B(0,-1),并且与x轴以及

 的图象与一次函数
的图象与一次函数 的图象交于点A(1,4)和点B
的图象交于点A(1,4)和点B ,
, ).
).
 >0时,直接写出
>0时,直接写出 >
>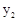 时自变量
时自变量
 时,求∠ODB的正切值.
时,求∠ODB的正切值.