题目内容
【题目】四边形ABCD中,DC∥AB,∠D=2∠B,CD=3,AD=2,求AB的长度.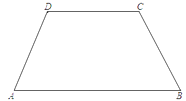
【答案】解:如图,过点A作 ![]() ,交CD的延长线于点E;
,交CD的延长线于点E;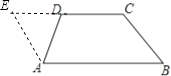
∵ ![]()
∴四边形ABCE为平行四边形,
∴∠E=∠B,AB=CE;
∵∠D=2∠B=2∠E,而∠D=∠E+∠EAD,
∴∠E=∠EAD,ED=AD=2,
∴EC=2+3=5,即AB=5.
∴AB的长度是5.
【解析】根据已知添加辅助线,过点A作 AE∥BC ,交CD的延长线于点E;,先根据两组对边分别平行的四边形是平行四边形,证明四边形ABCE为平行四边形,得出∠E=∠B,AB=CE,再利用三角形的外角性质证明∠E=∠EAD,得出ED=AD,再根据EC=AB求出AB的长度即可。
【考点精析】本题主要考查了三角形的外角和平行四边形的判定与性质的相关知识点,需要掌握三角形一边与另一边的延长线组成的角,叫三角形的外角;三角形的一个外角等于和它不相邻的两个内角的和;三角形的一个外角大于任何一个和它不相邻的内角;若一直线过平行四边形两对角线的交点,则这条直线被一组对边截下的线段以对角线的交点为中点,并且这两条直线二等分此平行四边形的面积才能正确解答此题.

练习册系列答案
 小天才课时作业系列答案
小天才课时作业系列答案 一课四练系列答案
一课四练系列答案 黄冈小状元满分冲刺微测验系列答案
黄冈小状元满分冲刺微测验系列答案 新辅教导学系列答案
新辅教导学系列答案 阳光同学一线名师全优好卷系列答案
阳光同学一线名师全优好卷系列答案
相关题目