题目内容
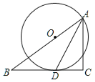
【题目】如图,![]() 中,
中,![]() 是
是![]() 的角平分线,
的角平分线,![]() 是
是![]() 上一点,以点
上一点,以点![]() 为圆心,
为圆心,![]() 的长为半径作
的长为半径作![]() 与
与![]() 相切于点
相切于点![]() .
.
(1)求证:![]() =
=![]()
(2)若________=![]() ,________=
,________=![]() ,填空
,填空
①![]() ________的半径长为________;
________的半径长为________;
②![]() ________=________.
________=________.
【答案】(1)见解析;(2)![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]()
【解析】
(1)连接OD,如图,先证明OD∥AC,再根据切线的性质得到OD⊥BC,则AC⊥BC,从而可判断∠ACB=90°;
(2)根据题意,若AC=3,BC=4,①先利用勾股定理计算出AB=5,设⊙O的半径为r,则OA=OD=r,OB=5-r,证明△BDO∽△BCA,利用相似比得到![]() ,然后解关于r的方程即可;
,然后解关于r的方程即可;
②利用△BDO∽△BCA得到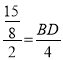 ,则可计算出BD=
,则可计算出BD=![]() ,从而得到CD=
,从而得到CD=![]() ,然后根据正切的定义计算tan∠CAD的值.
,然后根据正切的定义计算tan∠CAD的值.
证明:(1)连接![]() ,如图,
,如图,
∵![]() 是
是![]() 的角平分线,
的角平分线,
∴![]() =
=![]() ,
,
∵![]() =
=![]() ,
,
∴![]() =
=![]() ,
,
∴![]() =
=![]() ,
,
∴![]() ,
,
∵![]() 与
与![]() 相切于点
相切于点![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() =
=![]() ;
;
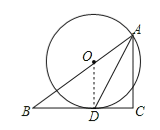
(2)①在Rt△ABC中,AB=![]() ,
,
设⊙O的半径为r,则OA=OD=r,OB=5-r,
∵OD∥AC,
∴△BDO∽△BCA,
∴![]() ,即
,即![]() ,
,
解得:![]() ,
,
即⊙O的半径为:![]() ;
;
②∵△BDO∽△BCA,
∴![]() ,即
,即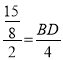 ,
,
解得:BD=![]() ,
,
∴CD=![]() ,
,
在Rt△ACD中,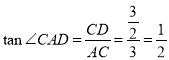 ;
;
故答案为:![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() .
.

练习册系列答案
 走进文言文系列答案
走进文言文系列答案
相关题目
【题目】已知二次函数y=ax2+bx+c中,函数y与自变量x的部分对应值如表:
x | … | ﹣2 | ﹣1 | 0 | 1 | 2 | 3 | … |
y | … | ﹣8 | ﹣3 | 0 | 1 | 0 | ﹣3 | … |
若A(m,y1),B(m﹣1,y2)两点都在该函数的图象上,当m满足范围_____时,y1<y2.