题目内容
【题目】已知![]() 是等边三角形,点
是等边三角形,点![]() 是
是![]() 的中点,
的中点,![]() 点在射线
点在射线![]() 上,
上,![]() 点在射线
点在射线![]() 上,
上,![]() ,
,
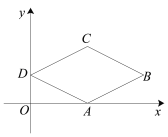
(1)如图1,若![]() 点与点
点与点![]() 重合,求证:
重合,求证:![]() .
.
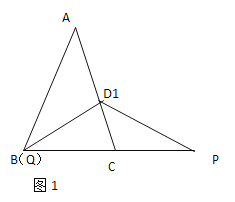
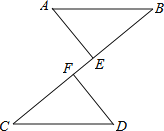
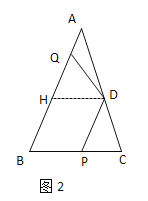
(2)如图2,若点![]() 在线段
在线段![]() 上,点
上,点![]() 在线段
在线段![]() 上,
上,![]() 求
求![]() 的值.
的值.

【答案】(1)见解析(2)12.
【解析】
(1)由等边三角形和等腰三角形的性质得出∠DBC=∠P,即可得出DB=DE;
(2)过点D作DH∥BC,交AB于点 H,证明△DQH≌△DPC(ASA),得出HQ=CP,得出BQ+BP=BH+HQ+BP=BH+BP+PC=BH+BC=![]() 即可求解.
即可求解.
(1)证明:∵△ABC 为等边三角形,
∴BA=BC,∠ABC=60![]() ,
,
∵D为AC的中点,
∴DB 平分∠ABC,
∴∠DBC=30![]() ,
,
∵![]()
∴∠P=180![]() 120
120![]() 30
30![]() =30
=30![]()
∴∠DBC=∠P,
∴DB=DP
(2)过点D作DH∥BC,交AB于点 H,如图2所示:
∵△ABC 为等边三角形,
∴∠A=∠B=∠C=60![]() ,
,
∵DH∥BC,
∴∠AHD=∠B=60![]() ,∠ADH=∠C=60
,∠ADH=∠C=60![]() ,
,
∴∠AHD=∠ADH=∠C=60![]() ,∠HDC=120
,∠HDC=120![]() ,
,
∴△ADH 是等边三角形,
∴DH=AD,
∵D为AC 的中点,
∴DA=DC,
∴DH=DC,
∵∠PDQ=120![]() ,∠HDC=120
,∠HDC=120![]() ,
,
∴∠PDH+∠QDH=∠PDH+∠CDP,
∴∠QDH=∠CDP,
在△DQH 和△DPC 中,
 ,
,
∴△DQH≌△DPC,
∴HQ=CP,
∴BQ+BP=BH+HQ+BP=BH+BP+PC=BH+BC=![]() =12,
=12,
即![]() =12.
=12.

练习册系列答案
相关题目