题目内容
【题目】点![]() 是双曲线
是双曲线![]() 上一点,点
上一点,点![]() 是双曲线
是双曲线![]() 上一点,
上一点,![]() 轴上有两点
轴上有两点![]() ,
,![]() ,平行四边形
,平行四边形![]() 的面积为
的面积为![]() ,则
,则![]() 的值是________.
的值是________.
【答案】![]() 或
或![]() 或
或![]() 或
或![]()
【解析】
设A的坐标是(x,y),过A作AM⊥x轴于M,过B作BN⊥x轴于N,则xy=2,根据图形结合平行四边形的性质,全等三角形的性质求出即可.
设A的坐标是(x,y),过A作AM⊥x轴于M,过B作BN⊥x轴于N,
则xy=2,
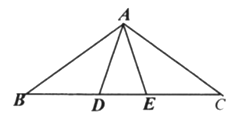
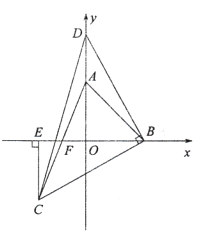
分为四种情况:①如图1,
B在第三象限时,
∵平行四边形ACBD的面积是6,
∴CDy=3,
∵xy=2,
∴ONy=2+3=5,
∴k=5;
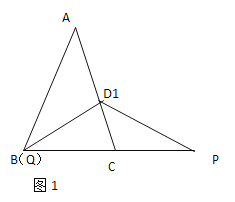
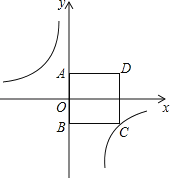
②如图2,
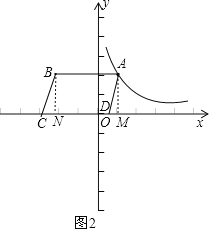
当B在第二重象限时,
∵△CBN的面积和△ADM的面积相等,
∴CN=DM,
∴AB×BN=6,
∵OM×AM=xy=2,
∴ON×BN=6-2=4,
∴k=-4;
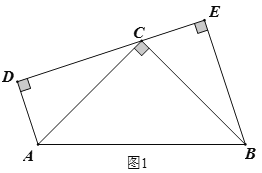
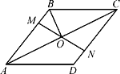
③如图3,

当B在第四象限时,∵△ACD和△BCD的面积相等,是3,
∴A、B的纵坐标互为相反数,横坐标相等,
即此时k=-2;
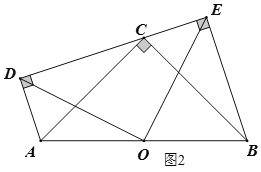
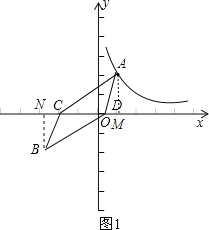
④如图4,

当B在第一象限时,AB∥CD,
∵OM×AM=2,CN×BN=6,
△CAM和△DBN面积相等,
∴ON×BN=(OM+MN)×BN=OM×AM+MN×BN=2+6=8,
即k=8;
故答案为:5或-2或-4或8.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案【题目】垫球是排球队常规训练的重要项目之一.下列图表中的数据是甲、乙、丙三人每人十次垫球测试的成绩.测试规则为连续接球10个,每垫球到位1个记1分.
运动员甲测试成绩表
测试序号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
成绩(分) | 7 | 6 | 8 | 7 | 7 | 5 | 8 | 7 | 8 | 7 |
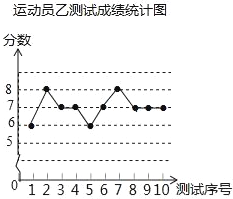
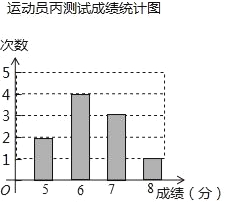
(1)写出运动员甲测试成绩的众数为_____;运动员乙测试成绩的中位数为_____;运动员丙测试成绩的平均数为_____;
(2)经计算三人成绩的方差分别为S甲2=0.8、S乙2=0.4、S丙2=0.8,请综合分析,在他们三人中选择一位垫球成绩优秀且较为稳定的接球能手作为自由人,你认为选谁更合适?为什么?
(3)甲、乙、丙三人相互之间进行垫球练习,每个人的球都等可能的传给其他两人,球最先从甲手中传出,第三轮结束时球回到甲手中的概率是多少?(用树状图或列表法解答)