题目内容
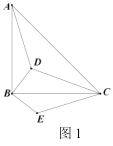
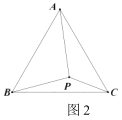
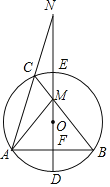
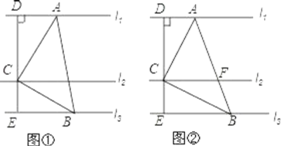
【题目】探究:如图①,直线l1∥l2∥l3,点C在l2上,以点C为直角顶点作∠ACB=90°,角的两边分别交l1与l3于点A、B,连结AB,过点C作CD⊥l1于点D,延长DC交l3于点E.
(1)求证:△ACD∽△CBE.
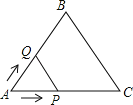
(2)应用:如图②,在图①的基础上,设AB与l2的交点为F,若AC=BC,l1与l2之间的距离为2,l2与l3之间的距离为1,则AF的长度是 .
【答案】(1)见解析;(2)![]()
【解析】
(1)根据已知条件得到∠ADC=∠CEB=90°,于是得到∠ACD+∠DAC=90°,由于∠ACB=90°,于是得到∠ACD+∠ECB=90°,根据余角的性质得到∠DAC=∠ECB,即可得到结论;
(2)通过△ACD≌△BCE,得到AD=CE=1,CD=BE=2,根据勾股定理得到AC=BC=![]() ,AB=
,AB=![]() ,然后根据平行线分线段成比例即可得到结论.
,然后根据平行线分线段成比例即可得到结论.
(1)∵l1∥l3,CD⊥l1,
∴∠ADC=∠CEB=90°,
∴∠ACD+∠DAC=90°,
∵∠ACB=90°,
∴∠ACD+∠ECB=90°,
∴∠DAC=∠ECB,
∴△ACD∽△CBE;
(2)在△ACD与△CBE中,
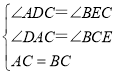 ,
,
∴△ACD≌△BCE,
∴AD=CE=1,CD=BE=2,
∵∠ADC=CEB=90°,
∴AC=BC=![]() ,
,
∵∠ACB=90°,
∴AB=![]() ,
,
∵l1∥l2∥l3,
∴![]() ,
,
∴AF=![]() .
.
故答案为:![]() .
.

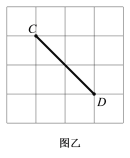
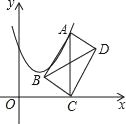
【题目】在方格纸中,每个方格的顶点叫做格点,以格点连线为边的三角形叫做格点三角形.如图甲中,每个小正方形的边长为1,以线段AB为一边的格点三角形随着第三个顶点的位置不同而发生变化.
(1)根据图甲,填写下表,并计算出格点三角形面积的平均值;
格点三角形面积 | 1 | 2 | 3 | 4 |
频数 |
(2)在图乙中,所给的方格纸大小与图甲一样,如果以线段CD为一边,作格点三角形,试填写下表,并计算出格点三角形面积的平均值;
格点三角形面积 | 1 | 2 | 3 | 4 |
频数 |
(3)如果将图乙中格点三角形面积记为s,频数记为x,根据你所填写的数据,猜测s与x之间存在哪种函数关系,并求出函数关系式.