题目内容
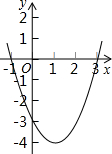 如图,抛物线与x轴交于点(-1,0)和(3,0),与y轴交于点(0,-3)则此抛物线对此函数的表达式为( )
如图,抛物线与x轴交于点(-1,0)和(3,0),与y轴交于点(0,-3)则此抛物线对此函数的表达式为( )分析:由抛物线与x轴的两交点坐标的横坐标,设出抛物线的两根形式y=a(x-x1)(x-x2),然后再把抛物线与y轴的交点坐标代入所设的解析式中,确定出a的值,进而得到抛物线的解析式,化为一般式即可.
解答:解:由抛物线与x轴交于点(-1,0)和(3,0),
设此抛物线的解析式为y=a(x+1)(x-3),
又抛物线与y轴交于(0,-3),
把x=0,y=-3代入y=a(x+1)(x-3)得:-3=a(0+1)(0-3),
即-3a=-3,解得:a=1,
则抛物线的解析式为y=(x+1)(x-3)=x2-2x-3.
故选B.
设此抛物线的解析式为y=a(x+1)(x-3),
又抛物线与y轴交于(0,-3),
把x=0,y=-3代入y=a(x+1)(x-3)得:-3=a(0+1)(0-3),
即-3a=-3,解得:a=1,
则抛物线的解析式为y=(x+1)(x-3)=x2-2x-3.
故选B.
点评:此题考查了待定系数法求二次函数的解析式,待定系数法求函数解析式的步骤一般为:设,代,求,答,此题的关键是设出抛物线的两根式y=a(x-x1)(x-x2),抛物线与x轴交点的横坐标即为两根式中的x1与x2.同时注意最后结果应化为一般式.

练习册系列答案
相关题目
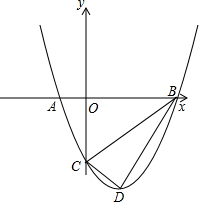 如图,抛物线与x轴交于A(-1,0)、B(3,0)两点,与y轴交于点C(0,-3),设抛物线的顶点为D.
如图,抛物线与x轴交于A(-1,0)、B(3,0)两点,与y轴交于点C(0,-3),设抛物线的顶点为D.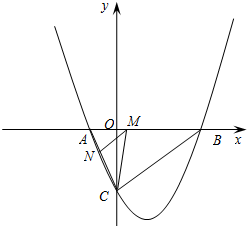 如图,抛物线与x轴交于A(x1,0)、B(x2,0)两点,且x1<x2,与y轴交于点C(0,-4),其中x1,x2是方程x2-4x-12=0的两个根.
如图,抛物线与x轴交于A(x1,0)、B(x2,0)两点,且x1<x2,与y轴交于点C(0,-4),其中x1,x2是方程x2-4x-12=0的两个根. (2012•历下区一模)如图,抛物线与x轴交于A(-1,0),B(4,0)两点,与y轴交于C(0,3),M是抛物线对称轴上的任意一点,则△AMC的周长最小值是
(2012•历下区一模)如图,抛物线与x轴交于A(-1,0),B(4,0)两点,与y轴交于C(0,3),M是抛物线对称轴上的任意一点,则△AMC的周长最小值是 如图,抛物线与y轴交于点A(0,4),与x轴交于B、C两点.其中OB、OC是方程的x2-10x+16=0两根,且OB<OC.
如图,抛物线与y轴交于点A(0,4),与x轴交于B、C两点.其中OB、OC是方程的x2-10x+16=0两根,且OB<OC.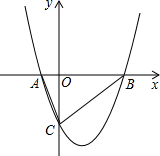 如图,抛物线与x轴交于A、B(6,0)两点,且对称轴为直线x=2,与y轴交于点C(0,-4).
如图,抛物线与x轴交于A、B(6,0)两点,且对称轴为直线x=2,与y轴交于点C(0,-4).