题目内容
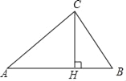
【题目】如图,学校有一块三角形草坪,数学课外小组的同学测得其三边的长分别为AB=200米,AC=160米,BC=120米.
(1)小明根据测量的数据,猜想△ABC是直角三角形,请判断他的猜想是否正确,并说明理由;
(2)若计划修一条从点C到BA边的小路CH,使CH⊥AB于点H,求小路CH的长.
【答案】(1)正确;(2)小路CH的长为96m.
【解析】
(1)直接利用勾股定理的逆定理分析得出答案;
(2)利用直角三角形面积求法得出CH的长.
(1)正确,
理由:在△ABC中,AB=200米,AC=160米,BC=120米,
∵AC2+BC2=1602+1202=2002=AB2,
即AC2+BC2=AB2,
∴△ABC是直角三角形;
(2)∵CH⊥AB,
∴S△ABC=![]() ABCH,
ABCH,
由(1)知,△ABC是直角三角形,
∵∠ABC=90°,
∴S△ABC=![]() ACBC,
ACBC,
∴ABCH=ACBC,
即160×120=200CH,
解得:CH=96,
答:小路CH的长为96m.

练习册系列答案
 第三学期赢在暑假系列答案
第三学期赢在暑假系列答案 学练快车道快乐假期暑假作业新疆人民出版社系列答案
学练快车道快乐假期暑假作业新疆人民出版社系列答案
相关题目
【题目】如图所示的是用棋子成的T字形图案:
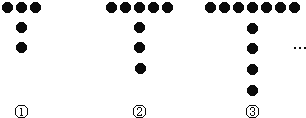
(1)填写下表:
图案序号 | ① | ② | ③ | ④ | …… | ⑧ |
每个图案中棋子的个数 | 5 | 8 | …… |
(2)第![]() 个“T“字形图案中棋子的个数为多少 (用含
个“T“字形图案中棋子的个数为多少 (用含![]() 的代数式表示);
的代数式表示);
(3)第20个“T”字形图案共有棋子多少个?
(4)计算前20个“T”字形图案中棋子的总个数.