题目内容
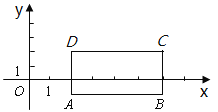
【题目】如图,点A在直线l外,点B在直线l上.
(1)在l上求作一点C,在l外求作一点D,使得以A、B、C、D为顶点的四边形是菱形;(要求:用直尺和圆规作出所有大小不同的菱形)
(2)连接AB,若AB=5,且点A到直线l的距离为4,通过计算,找出(1)中面积最小的菱形.

【答案】(1)见解析;(2)见解析
【解析】
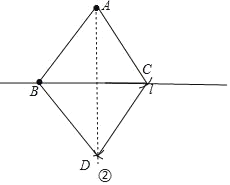
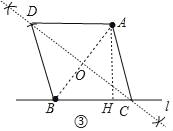
(1)以AB、BC为边作菱形得到如图①的菱形ABCD;以AB为边,BC为对角线作菱形得到如图②的菱形ABDC;以AB为对角线、BC为边作菱形得到如图③的菱形ACBD;
(2)分别进行三个菱形的面积可判断菱形ACBD的面积最小.
解:(1)如图①②③;
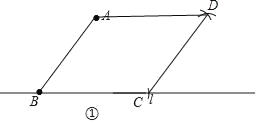
(2)图①中,菱形ABCD的面积=5×4=20,
图②中,BC=6,AD=8,菱形ABDC的面积=![]() ×6×8=24,
×6×8=24,
图③中,作AH⊥BC于H,设菱形的边长为x,
在Rt△ABH中,AH=4,AB=5,则BH=3,
所以CH=x﹣3,
在Rt△ACH中,42+(x﹣3)2=x2,解得x=![]()
菱形ACBD的面积=![]() ,
,
所以面积最小的菱形为ACBD.

练习册系列答案
相关题目