题目内容
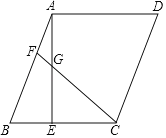
【题目】以点A为顶点作等腰Rt△ABC，其中∠BAC=∠DAE=90°，如图1所示放置，使得一直角边重合，连接BD、CE,延长BD交CE于点F.
（1）试判断BD、CE的关系，并说明理由；
（2）把两个等腰直角三角形按如图2所示放置，（1）中的结论是否仍成立？请说明理由.
【答案】（1）CE⊥BD，见解析；（2）仍然成立，见解析.
【解析】
（1）根据SAS证明△EAC与△DAB全等，再利用全等三角形的性质解答即可；
（2）先利用全等三角形的性质得出
根据（1）中的证明步骤解答即可
解：证明：（1）
，且CE⊥BD.理由如下：
∵等腰
，等腰
，
，
，
在
与
中，
，
，
；
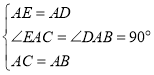∵ △EAC≌△DAB ，
，
，
，
,
∴CE⊥BD
（2）仍然成立.
∵等腰，等腰，
，，
在与中，
，
，
；
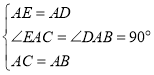∴△EAC≌△DAB，
，
，
，
．
∴CE⊥BD.
练习册系列答案
名校课堂系列答案
相关题目
