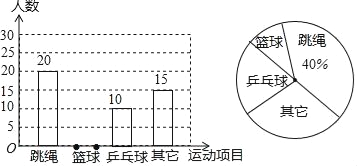
题目内容
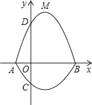
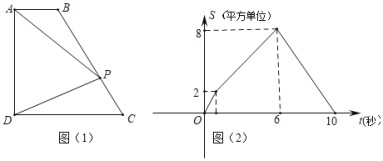
【题目】如图(1),四边形ABCD中,AB∥CD,∠ADC=90°,P从A点出发,以每秒1个单位长度的速度,按A→B→C→D的顺序在边上匀速运动,设P点的运动时间为t秒,△PAD的面积为S,S关于t的函数图象如图(2)所示,当P运动到BC中点时,△PAD的面积为( )
A. 4B. 5C. 6D. 7
【答案】B
【解析】
根据函数图象和三角形面积得出AB+BC=6,CD=4,AD=4,AB=1,当P运动到BC中点时,梯形ABCD的中位线也是△APD的高,求出梯形ABCD的中位线长,再代入三角形面积公式即可得出结果.
解:根据题意得:四边形ABCD是梯形,AB+BC=6,CD=10-6=4,
∵![]() AD×CD=8,
AD×CD=8,
∴AD=4,
又∵![]() AD×AB=2,
AD×AB=2,
∴AB=1,
当P运动到BC中点时,梯形ABCD的中位线也是△APD的高,
∵梯形ABCD的中位线长=![]() (AB+CD)=
(AB+CD)=![]() ,
,
∴△PAD的面积![]()
故选:B.

 智慧课堂密卷100分单元过关检测系列答案
智慧课堂密卷100分单元过关检测系列答案【题目】由于雾霾天气频发,市场上防护口罩出现热销.某药店准备购进一批![]() 两种不同型号口罩进行销售.下表是甲、乙两人购买
两种不同型号口罩进行销售.下表是甲、乙两人购买![]() 两种型号口罩的情况:
两种型号口罩的情况:
A型号数量(单位:个) | B型号数量(单位:个) | 总售价(单位:元) | |
甲 | 1 | 3 | 26 |
乙 | 3 | 2 | 29 |
(1)求一个![]() 型口罩和一个
型口罩和一个![]() 型口罩的售价各是多少元?
型口罩的售价各是多少元?
(2)药店准备购进这两种型号的口罩共50个,其中![]() 型口罩数量不少于35个,且不多于
型口罩数量不少于35个,且不多于![]() 型口罩的3倍,有几种购买方案?请写出购买方案.
型口罩的3倍,有几种购买方案?请写出购买方案.
(3)在(2)的条件下,药店在销售完这批口罩后,总售价能否达到282元?
【题目】小龙在学校组织的社会调查活动中负贵了解他所居住的小区450户居民的家庭收入情况从中随机调查了40户居民家庭收入情况(收入取整数,单位:元),并绘制了如下的频数分布表和频分布直方图。

分组 | 频数 | 百分比 |
600≤ | 2 | 5% |
800≤ | 6 | 15% |
1000≤ | 45% | |
9 | 22.5% | |
1400≤ | ||
1600≤ | 2 | |
合计 | 40 | 100% |
根据以上提供的信息,解答下列问题
(1)补全频数分布表
(2)补全频数分布直方图
(3)请你估计该居民小区家庭属于中等收入(大于1000不足1600元)的大约有多少户