题目内容
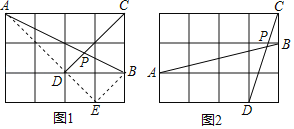
【题目】如图，在正方形ABCD中，E，F分别是边BC、CD上的点，BE=CF，AF与DE相交于点O，CG⊥DE，垂足为G.，求证：AD
=AOAF；
【答案】见解析
【解析】
通过证明△ADF≌△DCE，得出∠DAF=∠EDC，而∠EDC+∠ADE=90°，利用互余关系得出∠AOD=90°，然后可以证得△ADO∽△ADF，所以由该相似三角形的对应边成比例来证得结论；
证明：∵四边形ABCD为正方形，
∴AD=DC=BC,∠ADF=∠DCE=90°，
∵BE=CF，
∴DF=EC.
∴在△ADF与△DCE中，
，
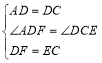∴△ADF≌△DCE(SAS)，
∴∠DAF=∠EDC，
又∵∠EDC+∠ADE=90°，
∴∠DAF +∠ADE =90°，
∴∠AOD=90°，
∴△ADO∽△AFD，
∴
,即AD
=AOAF；
练习册系列答案
金牌教辅培优优选卷期末冲刺100分系列答案
相关题目
