题目内容
【题目】如图,直线![]() 与
与![]() 轴、
轴、![]() 轴分别相交于点A和B.
轴分别相交于点A和B.
(1)直接写出坐标:点A ,点B ;
(2)以线段AB为一边在第一象限内作□ABCD,其顶点D(![]() ,
, ![]() )在双曲线
)在双曲线![]() (
(![]() >
>![]() )上.
)上.
①求证:四边形ABCD是正方形;
②试探索:将正方形ABCD沿![]() 轴向左平移多少个单位长度时,点C恰好落在双曲线
轴向左平移多少个单位长度时,点C恰好落在双曲线![]() (
(![]() >
>![]() )上.
)上.
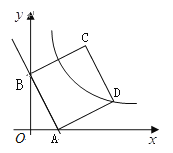
【答案】(1)A![]() ,B
,B![]() ;(2)①证明见解析②点C恰好落在双曲线
;(2)①证明见解析②点C恰好落在双曲线![]() (
(![]() >
>![]() )上.
)上.
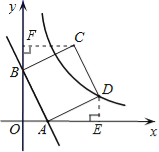
【解析】试题分析:(1)分别令x=0,求出y的值;令y=0,求出x的值即可得出点B与点A的坐标;
(2)①过点D作DE⊥x轴于点E,由全等三角形的性质可得出△AOB≌△DEA,故可得出AB=AD,再利用待定系数法求出直线AD的解析式即可得出AB⊥AD,由此可得出结论;
②过点C作CF⊥y轴,利用△AOB≌△DEA,同理可得出:△AOB≌△BFC,即可得出C点纵坐标,如果点在图象上,利用纵坐标求出横坐标即可.
解:(1)∵令x=0,则y=2;令y=0,则x=1,
∴A(1,0),B(0,2).
故答案为:(1,0),(0,2);
(2)①过点D作DE⊥x轴于点E,
∵A(1,0),B(0,2),D(3,1),
∴AE=OB=2,OA=DE=1,
在△AOB与△DEA中,
![]() ,
,
∴△AOB≌△DEA(SAS),
∴AB=AD,
设直线AD的解析式为y=kx+b(k≠0),
∴![]() ,
,
解得![]() ,
,
∵(﹣2)×=﹣1,
∴AB⊥AD,
∵四边形ABCD是正方形;
②过点C作CF⊥y轴,
∵△AOB≌△DEA,
∴同理可得出:△AOB≌△BFC,
∴OB=CF=2
∵C点纵坐标为:3,
代入y=,
∴x=1,
∴应该将正方形ABCD沿X轴向左平移2﹣1=1个单位长度时,点C的对应点恰好落在(1)中的双曲线上.

练习册系列答案
相关题目