��Ŀ����
����Ŀ��Ϊ��Ӧ���ҵ������ܼ��������ߣ�ij���ҿ�����һ�����͵ĵ綯������ͼ�����Ĵ��A����Ĺ���AB��AC�����MN�ļнǷֱ�Ϊ22����31����AT��MN������ΪT�������������Ŀ���BC�ij�Ϊ![]() m��
m��
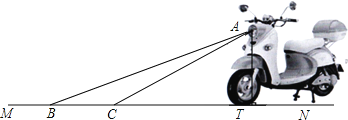
��1����BT�ij����������������أ���
��2��һ�������˴ӷ���Σ�յ�����ɲ�������ķ�Ӧʱ����0.2s���ӷ���Σ�յ��綯����ȫͣ������ʻ�ľ��������С��ȫ���룮ij����20km/h���ٶȼ�ʻ�ó���������ɲ���������綯��ֹͣ��ɲ��������![]() �����жϸó���Ƶ�����Ƿ���������С��ȫ�����Ҫ�����ǰ��ǰ�˼�ˮƽ������Բ��ƣ�����˵�����ɣ�
�����жϸó���Ƶ�����Ƿ���������С��ȫ�����Ҫ�����ǰ��ǰ�˼�ˮƽ������Բ��ƣ�����˵�����ɣ�
���ο����ݣ�sin22���![]() ��tan22���
��tan22���![]() ��sin31���
��sin31���![]() ��tan31���
��tan31���![]() ��
��
���𰸡���1��BT=![]() ����2���ó���Ƶ���Ʋ���������С��ȫ�����Ҫ�������ɼ�������
����2���ó���Ƶ���Ʋ���������С��ȫ�����Ҫ�������ɼ�������
��������
�����������1����ֱ����ACT�У��������Ǻ����Ķ��壬��AT=3x����CT=5x����ֱ����ABT���������Ǻ��������з�����⣻
��2�����������������Ӧ�����е綯����ʻ��·�̣�����ɲ�����룬Ȼ����BT�ij����бȽϼ��ɣ�
�⣺��1���������⼰ͼ֪����ACT=31������ABT=22��
��AT��MN
���ATC=90��
��Rt��ACT����ACT=31��
��tan31��=![]()
����AT=3x����CT=5x
��Rt��ABT����ABT=22��
��tan22��=![]()
����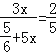
��ã�![]()
��![]() ��
��
��![]() ��
��
��2��![]() ��
��
![]() ��
��
![]()
���ó���Ƶ���Ʋ���������С��ȫ�����Ҫ��