题目内容
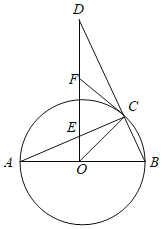
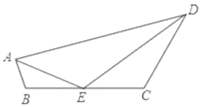
【题目】如图,已知BD为⊙O的直径,AB为⊙O的一条弦,过⊙O外一点P作PO⊥AB,垂足为点C,且交⊙O于点N,PO的延长线交⊙O于点M,连接BM、AD、AP.
(1)求证:PM∥AD;
(2)若∠BAP=2∠M,求证:PA是⊙O的切线;
(3)若AD=6,tan∠M=![]() ,求⊙O的半径.
,求⊙O的半径.
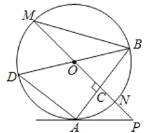
【答案】(1)见解析;(2)见解析;(3)⊙O的半径为5
【解析】
(1)由圆周角定理推出同位角相等,即可证明;
(2)根据切线的判定定理,证明![]() 即可;
即可;
(3)连接![]() ,根据正切的意义设未知数表示MC、CM,证明
,根据正切的意义设未知数表示MC、CM,证明![]() ∽
∽![]() ,进而用未知数表示NC、OM、OC,建立半径与未知数之间的数量关系,根据OC是△BAD的中位线得OC=
,进而用未知数表示NC、OM、OC,建立半径与未知数之间的数量关系,根据OC是△BAD的中位线得OC=![]() AD=3,从而求出未知数,进而求出OM.
AD=3,从而求出未知数,进而求出OM.
(1)证明:∵![]() 是直径,
是直径,
∴![]() ,
,
∵![]() ,
,
∴![]() ,
,
∴PM∥AD;
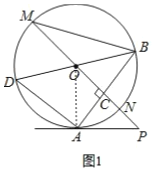
(2)证明:如图1,连接![]() ,
,
∵![]() ,
,
∴![]() ,
,
∴![]() ,
,
∵![]() ,
,
∴![]() ,
,
∵![]() ,
,
∴![]() ,
,
∴![]() ,
,
∵![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
∵![]() 是半径,
是半径,
∴![]() 是⊙O的切线;
是⊙O的切线;
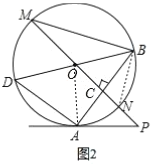
(3)如图2,连接![]() ,则
,则![]() ,
,
∵![]() ,
,
∴![]() ,
,
设![]() ,
,![]() ,
,
∵![]() 是⊙O直径,
是⊙O直径,![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() ∽
∽![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
∵![]() 是
是![]() 的中点,
的中点,![]() 是
是![]() 的中点,
的中点,![]() ,
,
∴![]() ,
,
解得:![]() ,
,
∴![]() ,
,
∴⊙O的半径为5.

练习册系列答案
相关题目