题目内容
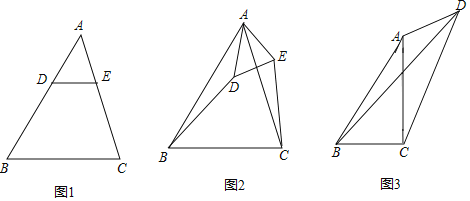
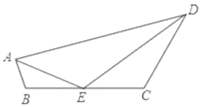
【题目】如图,四边形ABCD中,CD=BC=4,AB=1,E为BC中点,∠AED=120°,则AD的最大值是_____.
【答案】7
【解析】
如图,作出点B关于AE的对称点M,点C关于DE的对称点N,连接AM、EM,MN、DN、EN.证明△MNE是等边三角形即可解决问题.
解:如图,作出点B关于AE的对称点M,点C关于DE的对称点N,连接AM、EM,MN、DN、EN.
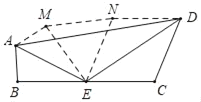
根据轴对称的性质可得:
AM=AB,BE=EM,CE=EN,DN=CD,∠AEB=AEM,∠DEC=∠DMN,
∵∠AED=120°,
∴∠AEB+∠DEC=180°﹣∠AED=180°﹣120°=60°,
∴∠MEN=∠AED﹣(∠AEM+∠DEN)=120°﹣60°=60°,
∵点M是四边形ABCD的边BC的中点,
∴BE=CE,
∴EM=EN,
∴△ENM是等边三角形,
∵AD≤AM+MN+DN,
∴AD≤7,
∴AD的最大值为7,
故答案为:7.

练习册系列答案
相关题目