Question

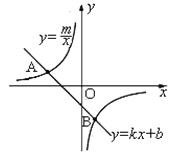
【题目】如图，A，B两点分别在反比例函数和的图像上，连接OA，OB，若OA⊥OB，OB=2OA，则k的值为（ ）

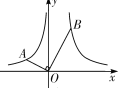
A.-2B.2C.-4D.4

Answer 1

【答案】D

【解析】

如图，过A、B分别作轴的垂线，垂足分别为E、F，先证明△AEO~△OFB，根据相似三角形性质得出OF=2AE，BF=2OE，设A(，)，代入得出，从而得出AEOE=，再设B(，)，然后进一步分析讨论即可.

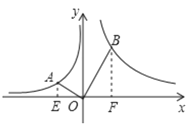
如图，过A、B分别作轴的垂线，垂足分别为E、F，

∵OA⊥OB，

∴∠AOE+∠BOF=90°，

∵∠AOE+∠OAE=90°，

∴∠OAE=∠BOF，

∵∠AEO=∠OFB=90°，

∴△AEO~△OFB，

∵OB=2OA，

∴，

∴OF=2AE，BF=2OE，

∴OF×BF=2AE×2OE=4 AE×OE，

∵点A在反比例函数上，

设A(，)，

则：，

∵OE=，AE=，

∴AE×OE=，

∵B点在反比例函数的图像上，

又设B(，)，

则：OF=，BF=，

∴OF×BF=，

∵OF×BF=4 AE×OE=4，

∴，

故选：D.