题目内容
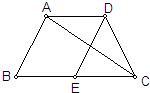27、已知：在梯形ABCD中，AD∥BC，CA平分∠DCE，AB⊥AC，E为BC的中点．求证：DE、AC互相垂直平分．
分析：此题要证明DE、AC互相垂直平分．则连接AE，只需证明四边形ADCE是菱形．根据已知条件首先运用两组对边分别平行的四边形是平行四边形，再根据一组邻边相等的平行四边形是菱形证明．
解答：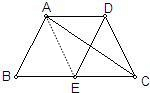
解：∵在直角三角形ABC中，E是BC的中点，
∴AE是RtABC的中线，
∴AE=CE=BE，
∴∠EAC=∠ACE．
∵AD∥BC
∴∠ACE=∠ACD
∴∠EAC=∠ACD
∴AE∥CD
∴四边形AECD是平行四边形．
又AE=CE
所以平行四边形AECD是菱形，
所以DE、AC互相垂直平分．
解：∵在直角三角形ABC中，E是BC的中点，∴AE是RtABC的中线，
∴AE=CE=BE，
∴∠EAC=∠ACE．
∵AD∥BC
∴∠ACE=∠ACD
∴∠EAC=∠ACD
∴AE∥CD
∴四边形AECD是平行四边形．
又AE=CE
所以平行四边形AECD是菱形，
所以DE、AC互相垂直平分．
点评：熟练掌握特殊四边形的性质和判定．
练习册系列答案
相关题目
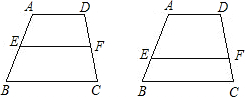已知：在梯形ABCD中，AD∥BC，点E在AB上，点F在DC上，且AD=a，BC=b．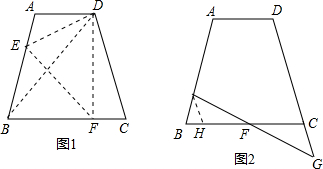
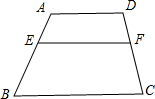如图，已知：在梯形ABCD中，AD∥BC，AD=3，BC=5，点E在AB上，且AE：EB=2：3，过点E作EF∥BC交CD于F，求EF的长？
已知：在梯形ABCD中，AD∥BC，AB=DC=5，AD=3.5，
已知，在梯形ABCD中，AD∥BC，∠ABC=90°，BC=2AD，点E、F分别是BC和DC的中点，连接AE、EF和BD，AE和BD相交于点G．