题目内容
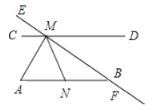
【题目】如图，∠CME+∠ABF＝180°，MA平分∠CMN．若∠MNA＝62°，求∠A的度数．根据提示将解题过程补充完整．
解：因为∠ABM+∠ABF＝180°，
又因为∠CME+∠ABF＝180°（已知），
所以∠ABM＝∠CME
所以AB∥CD，理由：（ ）
所以∠CMN+（ ）＝180°，
理由：（__________________________）
因为∠MNA＝62°，
所以∠CMN＝（ ）
因为MA平分∠CMN，
所以∠AMC＝
∠CMN =（ ）．（角平分线的定义）
因为AB∥CD，
所以∠A＝∠AMC＝（ ）理由：（__________________________________）
【答案】同位角相等，两直线平行；∠MNA；两直线平行，同旁内角互补；118°；59°；59°；两直线平行，内错角相等
【解析】
根据同角的补角相等可得出∠ABM＝∠CME，利用“同位角相等，两直线平行”可得出AB∥CD，由“两直线平行，同旁内角互补”及∠MNA =62°可求出∠CMN =118°，结合角平分线的定义可求出∠AMC的度数，再利用“两直线平行，内错角相等”即可求出∠A的度数．
解：因为∠ABM+∠ABF＝180°，
又因为∠CME+∠ABF＝180°（已知），
所以∠ABM＝∠CME
所以AB∥CD，（同位角相等，两直线平行）
所以∠CMN+∠MNA＝180°，（两直线平行，同旁内角互补）
因为∠MNA＝62°，
所以∠CMN＝118°，
因为MA平分∠CMN，
所以∠AMC＝
∠CMN =59°．（角平分线的定义）
因为AB∥CD，
所以∠A＝∠AMC＝59°（两直线平行，内错角相等）
故答案为：同位角相等，两直线平行；∠MNA；两直线平行，同旁内角互补；118°；59°；59°；两直线平行，内错角相等
