题目内容
【题目】已知,如图,二次函数y=ax2+2ax﹣3a(a≠0)图象的顶点为H,与x轴交于A、B两点(B在A点右侧),点H、B关于直线l: ![]() 对称.
对称. 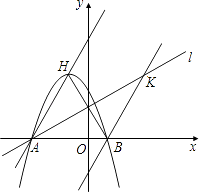
(1)求A、B两点坐标,并证明点A在直线l上;
(2)求二次函数解析式; 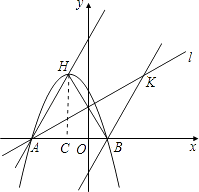
(3)过点B作直线BK∥AH交直线l于K点,M、N分别为直线AH和直线l上的两个动点,连接HN、NM、MK,求HN+NM+MK和的最小值. 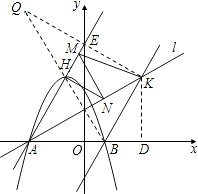
【答案】
(1)解:依题意,得ax2+2ax﹣3a=0(a≠0),
两边都除以a得:
即x2+2x﹣3=0,
解得x1=﹣3,x2=1,
∵B点在A点右侧,
∴A点坐标为(﹣3,0),B点坐标为(1,0),
答:A、B两点坐标分别是(﹣3,0),(1,0)
证明:∵直线l: ![]() ,
,
当x=﹣3时, ![]() ,
,
∴点A在直线l上
(2)解:∵点H、B关于过A点的直线l: ![]() 对称,
对称,
∴AH=AB=4,
过顶点H作HC⊥AB交AB于C点,
则 ![]() ,
, ![]() ,
,
∴顶点 ![]() ,
,
代入二次函数解析式,解得 ![]() ,
,
∴二次函数解析式为 ![]() ,
,
答:二次函数解析式为 ![]()
(3)解:直线AH的解析式为 ![]() ,
,
直线BK的解析式为 ![]() ,
,
由 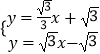 ,
,
解得 ![]() ,
,
即 ![]() ,
,
则BK=4,
∵点H、B关于直线AK对称,K(3,2 ![]() ),
),
∴HN+MN的最小值是MB,
过K作KD⊥x轴于D,作点K关于直线AH的对称点Q,连接QK,交直线AH于E,
则QM=MK, ![]() ,AE⊥QK,
,AE⊥QK,
∴根据两点之间线段最短得出BM+MK的最小值是BQ,即BQ的长是HN+NM+MK的最小值,
∵BK∥AH,
∴∠BKQ=∠HEQ=90°,
由勾股定理得QB= ![]() =
= ![]() =8,
=8,
∴HN+NM+MK的最小值为8,
答:HN+NM+MK和的最小值是8.
【解析】(1)求出方程ax2+2ax﹣3a=0(a≠0),即可得到A点坐标和B点坐标;把A的坐标代入直线l即可判断A是否在直线上;(2)根据点H、B关于过A点的直线l: ![]() 对称,得出AH=AB=4,过顶点H作HC⊥AB交AB于C点,求出AC和HC的长,得出顶点H的坐标,代入二次函数解析式,求出a,即可得到二次函数解析式;(3)解方程组
对称,得出AH=AB=4,过顶点H作HC⊥AB交AB于C点,求出AC和HC的长,得出顶点H的坐标,代入二次函数解析式,求出a,即可得到二次函数解析式;(3)解方程组 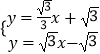 ,即可求出K的坐标,根据点H、B关于直线AK对称,得出HN+MN的最小值是MB,过点K作直线AH的对称点Q,连接QK,交直线AH于E,得到BM+MK的最小值是BQ,即BQ的长是HN+NM+MK的最小值,由勾股定理得QB=8,即可得出答案.
,即可求出K的坐标,根据点H、B关于直线AK对称,得出HN+MN的最小值是MB,过点K作直线AH的对称点Q,连接QK,交直线AH于E,得到BM+MK的最小值是BQ,即BQ的长是HN+NM+MK的最小值,由勾股定理得QB=8,即可得出答案.
【考点精析】解答此题的关键在于理解解二元一次方程组的相关知识,掌握二元一次方程组:①代入消元法;②加减消元法,以及对抛物线与坐标轴的交点的理解,了解一元二次方程的解是其对应的二次函数的图像与x轴的交点坐标.因此一元二次方程中的b2-4ac,在二次函数中表示图像与x轴是否有交点.当b2-4ac>0时,图像与x轴有两个交点;当b2-4ac=0时,图像与x轴有一个交点;当b2-4ac<0时,图像与x轴没有交点.

【题目】城区某中学为形成体育特色,落实学生每天![]() 小时的锻炼时间,通过调查研究,决定在七、八、九年级分别开展跳绳、羽毛球、毽球的健身运动.
小时的锻炼时间,通过调查研究,决定在七、八、九年级分别开展跳绳、羽毛球、毽球的健身运动.
国家规定初中每班的标准人数为![]() 人,七年级共有八个班,各班人数情况如下表,八年级学生人数是七年级学生人数的
人,七年级共有八个班,各班人数情况如下表,八年级学生人数是七年级学生人数的![]() 倍少
倍少![]() 人,九年级学生人数的
人,九年级学生人数的![]() 倍刚好是七、八年级学生人数的总和.(注:
倍刚好是七、八年级学生人数的总和.(注:![]() 班表示七年级一班)
班表示七年级一班)
班级 |
|
|
|
|
|
|
|
|
和每班标准 人数的差值 |
|
|
|
|
|
|
|
|
![]() 用含
用含![]() 的式子表示该中学七年级学生总数;
的式子表示该中学七年级学生总数;
![]() 学校决定按每人一根跳绳、一个毽球,两人一副羽毛球拍的标准,购买相应的体育器材以满足学生锻炼需要,其中跳绳每根
学校决定按每人一根跳绳、一个毽球,两人一副羽毛球拍的标准,购买相应的体育器材以满足学生锻炼需要,其中跳绳每根![]() 元,毽球每个
元,毽球每个![]() 元,羽毛球拍每副
元,羽毛球拍每副![]() 元.请你计算当
元.请你计算当![]() 时,学校为落实
时,学校为落实![]() 小时体育锻炼时间需购买器材的费用是多少?
小时体育锻炼时间需购买器材的费用是多少?
【题目】(本题10分)某自行车厂一周计划生产700辆自行车,平均每天生产自行车100辆,由于各种原因,实际每天生产量与计划每天生产量相比有出入。下表是某周的自行车生产情况(超计划生产量为正、不足计划生产量为负,单位:辆):
星期 | 一 | 二 | 三 | 四 | 五 | 六 | 日 |
增减 | +8 | -2 | -3 | +16 | -9 | +10 | -11 |
(1)根据记录可知前三天共生产自行车 辆;
(2)产量最多的一天比产量最少的一天生产 辆;
(3)若该厂实行按生产的自行车数量的多少计工资,即计件工资制。如果每生产一辆自行车就可以得人民币60 元,超额完多成任务,每超一辆可多得 15 元;若不足计划数的,每少生产一辆扣 15 元,那么该厂工人这一周的工资总额是多少?