题目内容
【题目】如图,已知:射线PO与⊙O交于A、B两点,PC、PD分别切⊙O于点C、D.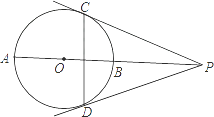
(1)请写出两个不同类型的正确结论;
(2)若CD=12,tan∠CPO= ![]() ,求PO的长.
,求PO的长.
【答案】
(1)解:不同类型的正确结论有:
①PC=PD,②∠CPO=∠DP,③CD⊥BA,④∠CEP=90°,⑤PC2=PAPB
(2)解:连接OC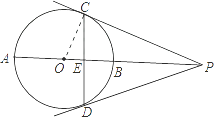
∵PC、PD分别切⊙O于点C、D
∴PC=PD,∠CPO=∠DPA
∴CD⊥AB
∵CD=12
∴DE=CE= ![]() CD=6.
CD=6.
∵tan∠CPO= ![]() ,
,
∴在Rt△EPC中,PE=12
∴由勾股定理得CP=6 ![]()
∵PC切⊙O于点C
∴∠OCP=90°
在Rt△OPC中,
∵tan∠CPO= ![]() ,
,
∴ ![]()
∴OC=3 ![]() ,
,
∴OP= ![]() =15
=15
【解析】(1)根据切线长定理可得出PC=PD,∠CPO=∠DP,根据等腰三角形三线合一的性质可得出CD⊥BA,∠CEP=90°,利用相似三角形的判定及性质可证得PC2=PAPB,即可得出答案。
(2)根据切线成定理可证出PC=PD,∠CPO=∠DPA,再根据等腰三角形的性质证得CD⊥AB,再根据垂径定理求出CE的长,在Rt△PCE中根据tan∠CPO= ![]() ,就可求出PE的长,利用勾股定理求出PC的长, 在Rt△PCO中根据tan∠CPO=
,就可求出PE的长,利用勾股定理求出PC的长, 在Rt△PCO中根据tan∠CPO= ![]() ,求出OC的长,然后利用勾股定理就可求出PO的长。
,求出OC的长,然后利用勾股定理就可求出PO的长。

练习册系列答案
 千里马走向假期期末仿真试卷寒假系列答案
千里马走向假期期末仿真试卷寒假系列答案
相关题目





