��Ŀ����
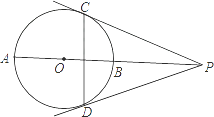
����Ŀ����֪����ͼ��ֱ��a��b��ֱ��c��ֱ��a��b�ֱ��ཻ��C��D���㣬ֱ��d��ֱ��a��b�ֱ��ཻ��A��B���㣬��P��ֱ��AB���˶�(����A��B�����غ�)��
(1)��ͼ1������P���߶�AB���˶�ʱ�����У���CPD����PCA+��PDB����˵�����ɣ�
(2)��ͼ2������P���߶�AB���ӳ������˶�ʱ����CPD����PCA����PDB֮����������������ϵ����˵�����ɣ�
(3)��ͼ3������P���߶�BA���ӳ������˶�ʱ����CPD����PCA����PDB֮������������������ϵ(ֻ��ֱ�Ӹ�������)��

���𰸡���1��֤������������2����CPD=��PCA����PDB�����ɼ���������3����CPD=��PDB����PCA��
��������
��1������P��a��ƽ���ߣ�����ƽ���ߵ����ʽ�����⣻
��2������P��b��ƽ����PE����ƽ���ߵ����ʿɵó�a��b��PE���ɴ˼��ɵó����ۣ�
��3����ֱ��AC��DP���ڵ�F������������ǵ����ʿɵó���1+��3=��PFA������ƽ���ߵ����ʼ��ɵó����ۣ�
��1��֤������ͼ1������P��PE��a�����1=��CPE��
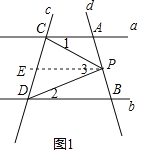
��a��b��PE��a��
��PE��b��
���2=��DPE��
���3=��1+��2��
����CPD=��PCA+��PDB��
��2����CPD=��PCA-��PDB��
���ɣ���ͼ2������P��PE��b�����2=��EPD��
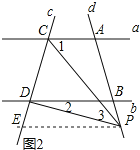
��ֱ��a��b��
��a��PE��
���1=��EPC��
�ߡ�3=��EPC-��EPD��
���3=��1-��2��
����CPD=��PCA-��PDB��
��3����CPD=��PDB-��PCA��
֤������ͼ3����ֱ��AC��DP���ڵ�F��
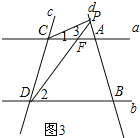
�ߡ�PFA����PCF����ǣ�
���PFA=��1+��3��
��a��b��
���2=��PFA��
���2=��1+��3��
���3=��2-��1��
����CPD=��PDB-��PCA��