题目内容
【题目】“转化”是数学中的一种重要思想,即把陌生的问题转化成熟悉的问题,把复杂的问题转化成简单的问题,把抽象的问题转化为具体的问题.
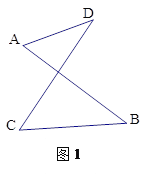
已知:如图1,线段AB、CD相交于点O,连接AD、CB,我们把形如图1的图形称之为“8字形”,试解答下列问题:
问题一:在图1中,请直接写出∠A、∠B、∠C、∠D之间的数量关系 ;
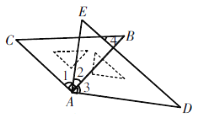
问题二:在图2中,若∠D=40°,∠B=36°,∠DAB和∠BCD的平分线AP和CP相交于点P,并且与CD、AB分别相交于M、N,试求∠P的度数;
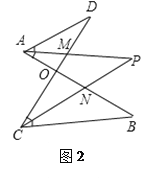
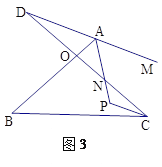
问题三:在图3中,已知AP、CP分别平分∠BAM、∠BCD,请问∠P与∠B、∠D之间存在着怎样的数量关系?并说明理由.
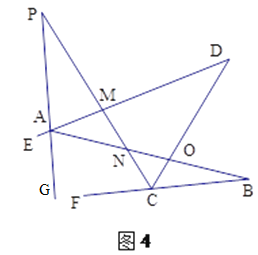
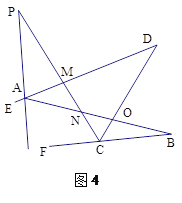
问题四:在图4中,已知AP的反向延长线平分∠EAB,CP平分∠DCF,请直接写出∠P与∠B、∠D之间的数量关系 .
【答案】(1)![]() (2)38°(3)
(2)38°(3)![]() (4)
(4) ![]()
【解析】分析:(1)利用三角形的内角和定理表示出∠AOD与∠BOC,再根据对顶角相等可得∠AOD=∠BOC,然后整理即可得解;
(2)根据(1)的关系式求出∠OCB﹣∠OAD,再根据角平分线的定义求出∠DAM﹣∠PCM,然后利用“8字形”的关系式列式整理即可得解;
(3)根据“8字形”数量关系有:∠P+∠PCN=∠D+∠DAN=∠D+180°-∠MAN①,∠B+2∠PCN=∠D+180°-2∠MAN②,由①和②即可得到结论;
(4)根据“8字形”数量关系有:∠P+∠PAN=∠B+∠BCN,∠D+∠DAN=∠B+∠BCO,即∠P+180°-∠GAN=∠B+180°-∠FCN①,∠D+180°-2∠GAN =∠B+180°-2∠FCN②,由①②可得结论.
详解:(1)在△AOD中,∠AOD=180°﹣∠A﹣∠D.在△BOC中,∠BOC=180°﹣∠B﹣∠C.
∵∠AOD=∠BOC(对顶角相等),∴180°﹣∠A﹣∠D=180°﹣∠B﹣∠C,∴∠A+∠D=∠B+∠C;
(2)∵∠D=40°,∠B=36°,∴∠OAD+40°=∠OCB+36°,∴∠OCB﹣∠OAD=4°.
∵AP、CP分别是∠DAB和∠BCD的角平分线,∴∠DAM=![]() ∠OAD,∠PCM=
∠OAD,∠PCM=![]() ∠OCB.
∠OCB.
又∵∠DAM+∠D=∠PCM+∠P,∴∠P=∠DAM+∠D﹣∠PCM=![]() (∠OAD﹣∠OCB)+∠D=
(∠OAD﹣∠OCB)+∠D=![]() ×(﹣4°)+40°=38°;
×(﹣4°)+40°=38°;
(3)根据“8字形”数量关系有:∠P+∠PCN=∠D+∠DAN=∠D+180°-∠MAN①,∠B+∠BCN=∠D+∠DAO=∠D+180°-∠MAB,∴∠B+2∠PCN=∠D+180°-2∠MAN②,由①和②得:∠D+∠B=2∠P-180°;
(4)根据“8字形”数量关系有:∠P+∠PAN=∠B+∠BCN,∠D+∠DAN=∠B+∠BCO,
∴∠P+180°-∠
由①②得:2∠P-∠B=∠D.