题目内容
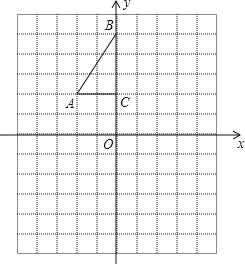
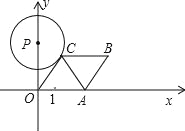
【题目】如图所示，已知A点从（1，0）点出发，以每秒1个单位长的速度沿着x轴的正方向运动，经过t秒后，以O、A为顶点作菱形OABC，使B．C点都在第一象限内，且AO=AC，又以P（0，
）为圆心，PC为半径的圆恰好与OC所在的直线相切，则t=（ ）.
A．
B．
C．5 D．7
【答案】C.
【解析】
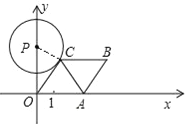
试题分析：先根据已知条件，求出经过t秒后，OC的长，当⊙P与OA，即与x轴相切时，如图所示，则切点为O，此时PC=OP，过P作PE⊥OC，利用垂径定理和解直角三角形的有关知识即可求出t的值．∵已知A点从（1，0）点出发，以每秒1个单位长的速度沿着x轴的正方向运动，∴经过t秒后，∴OA=1+t，∵四边形OABC是菱形，∴OC=1+t，∵⊙P恰好与OC所在的直线相切，∴PC⊥OC，∵AO=AC=OC，∴∠AOC=60°，∠COP=30°，在Rt△OPC中，OC=OPcos30°=
×
=6，∴1+t=6，∴t=5．
故选：C．
练习册系列答案
相关题目
