��Ŀ����
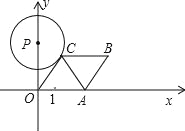
����Ŀ����ͼ����������ÿ���������ľ���Ϊһ����λ���ȣ���A��B��C��D��Ӧ�����ֱ���a��b��c��d����d��2a=14 ![]()
��1����ôa= �� b=��
��2����A��3����λ/����ٶ�����������������˶���1����B��4����λ/����ٶ�Ҳ����������������˶�������A����D�㴦���̷��أ����B�������ij�㴦��������������Ӧ������
��3�����A��B�����ԣ�2���е��ٶ�ͬʱ������ĸ������˶�����C��ͼ�ϵ�λ�ó���Ҳ������ĸ������˶�����ʼ�ձ���AB= ![]() AC������C�˶�����6ʱ����A��Ӧ�����Ƕ��٣�
AC������C�˶�����6ʱ����A��Ӧ�����Ƕ��٣�
���𰸡�
��1��-6��-8
��2���⣺�ɣ�1����֪��a=��6��b=��8��c=��3��d=2��
��A�˶���D��������ʱ��Ϊ ![]() ��
��
���˶���ʱ��Ϊt�룬
��A��Ӧ����Ϊ2��3��t�� ![]() ��=10��3t��
��=10��3t��
B��Ӧ����Ϊ����8+4��t��1��=4t��12��
��A��B��������ʱ��10��3t=4t��12��t= ![]() ��
��
��4t��12= ![]() ��
��
��������Ӧ����Ϊ ![]()
��3���⣺���˶���ʱ��Ϊt
A��Ӧ����Ϊ����6��3t
B��Ӧ����Ϊ����8��4t
��AB=|��6��3t������8��4t��|=|t+2|=t+2
��AB= ![]() AC��
AC��
��AC= ![]() AB=
AB= ![]() t+3��
t+3��
��C��Ӧ����Ϊ��6��
��AC=|��6������6��3t��|=|3t|= ![]() t+3��
t+3��
�ٵ�3t= ![]() t+3��t=2��
t+3��t=2��
�ڵ�3t+ ![]() t+3=0��t=��
t+3=0��t=�� ![]() ��������ʵ�������
��������ʵ�������
��t=2��
�ੁ6��3t=��12��
�𣺵�A��Ӧ����Ϊ��12
���������⣺��1����ͼ��֪��d=a+8��
��d��2a=14��
��a+8��2a=14��
���a=��6��
��b=a��2=��8��
�����㾫�����������⣬������Ҫ�˽�����(�����ǹ涨��ԭ�㡢������λ���ȵ�һ��ֱ��)��

 һ����������ϵ�д�
һ����������ϵ�д�