题目内容
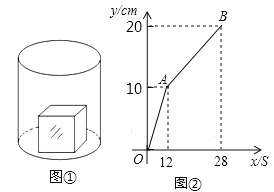
【题目】如图①,一个正方体铁块放置在圆柱形水槽内,现以一定的速度往水槽中注水,28s时注满水槽.水槽内水面的高度y(cm)与注水时间x(s)之间的函数图象如图②所示.
(1)正方体的棱长为 cm;
(2)求线段AB对应的函数解析式,并写出自变量x的取值范围;
(3)如果将正方体铁块取出,又经过t(s)恰好将此水槽注满,直接写出t的值.
【答案】(1)10;(2)y=![]() x+
x+![]() (12≤x≤28);(3)4秒
(12≤x≤28);(3)4秒
【解析】
试题分析:(1)直接利用一次函数图象结合水面高度的变化得出正方体的棱长;
(2)直接利用待定系数法求出一次函数解析式,再利用函数图象得出自变量x的取值范围;
(3)利用一次函数图象结合水面高度的变化得出t的值.
试题解析:(1)由题意可得:12秒时,水槽内水面的高度为10cm,12秒后水槽内高度变化趋势改变,
故正方体的棱长为10cm;
(2)设线段AB对应的函数解析式为:y=kx+b,
∵图象过A(12,0),B(28,20),
∴![]() ,
,
解得: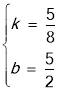 ,
,
∴线段AB对应的解析式为:y=![]() x+
x+![]() (12≤x≤28);
(12≤x≤28);
(3)∵28﹣12=16(cm),
∴没有立方体时,水面上升10cm,所用时间为:16秒,
∵前12秒由立方体的存在,导致水面上升速度加快了4秒,
∴将正方体铁块取出,经过4秒恰好将此水槽注满.

练习册系列答案
相关题目

