题目内容
【题目】如图,在Rt△ABC中,∠ACB=90°,∠A=45°,AB=4cm.点P从点A出发,以2cm/s的速度沿边AB向终点B运动.过点P作PQ⊥AB交折线ACB于点Q,D为PQ中点,以DQ为边向右侧作正方形DEFQ.设正方形DEFQ与△ABC重叠部分图形的面积是y(cm2),点P的运动时间为x(s).

(1)当点Q在边AC上时,正方形DEFQ的边长为 cm(用含x的代数式表示);
(2)当点P不与点B重合时,求点F落在边BC上时x的值;
(3)当0<x<2时,求y关于x的函数解析式;
(4)直接写出边BC的中点落在正方形DEFQ内部时x的取值范围.
【答案】(1)x;(2)x=![]() ;(3)见解析;(4)1<x<
;(3)见解析;(4)1<x<![]() .
.
【解析】
试题分析:(1)由已知条件得到∠AQP=45°,求得PQ=AP=2x,由于D为PQ中点,于是得到DQ=x;
(2)如图①,延长FE交AB于G,由题意得AP=2x,由于D为PQ中点,得到DQ=x,求得GP=2x,列方程于是得到结论;
(3)如图②,当0<x≤![]() 时,根据正方形的面积公式得到y=x2;如图③,当
时,根据正方形的面积公式得到y=x2;如图③,当![]() <x≤1时,过C作CH⊥AB于H,交FQ于K,则CH=
<x≤1时,过C作CH⊥AB于H,交FQ于K,则CH=![]() AB=2,根据正方形和三角形面积公式得到y=﹣
AB=2,根据正方形和三角形面积公式得到y=﹣![]() x2+20x﹣8;如图④,当1<x<2时,PQ=4﹣2x,根据三角形的面积公式得到结论;
x2+20x﹣8;如图④,当1<x<2时,PQ=4﹣2x,根据三角形的面积公式得到结论;
(4)当Q与C重合时,E为BC的中点,得到x=1,当Q为BC的中点时,BQ=![]() ,得到x=
,得到x=![]() ,于是得到结论.
,于是得到结论.
试题解析:(1)∵∠ACB=90°,∠A=45°,PQ⊥AB,
∴∠AQP=45°,
∴PQ=AP=2x,
∵D为PQ中点,
∴DQ=x,
(2)如图①,延长FE交AB于G,由题意得AP=2x,
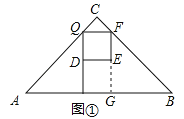
∵D为PQ中点,
∴DQ=x,
∴GP=2x,
∴2x+x+2x=4,
∴x=![]() ;
;
(3)如图②,当0<x≤![]() 时,y=S正方形DEFQ=DQ2=x2,
时,y=S正方形DEFQ=DQ2=x2,
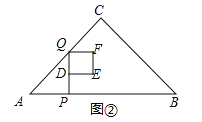
∴y=x2;
如图③,当![]() <x≤1时,过C作CH⊥AB于H,交FQ于K,则CH=
<x≤1时,过C作CH⊥AB于H,交FQ于K,则CH=![]() AB=2,
AB=2,

∵PQ=AP=2x,CK=2﹣2x,
∴MQ=2CK=4﹣4x,FM=x﹣(4﹣4x)=5x﹣4,
∴y=S正方形DEFQ﹣S△MNF=DQ2﹣![]() FM2,
FM2,
∴y=x2﹣![]() (5x﹣4)2=﹣
(5x﹣4)2=﹣![]() x2+20x﹣8,
x2+20x﹣8,
∴y=﹣![]() x2+20x﹣8;
x2+20x﹣8;
如图④,当1<x<2时,PQ=4﹣2x,
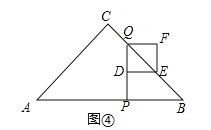
∴DQ=2﹣x,
∴y=S△DEQ=![]() DQ2,
DQ2,
∴y=![]() (2﹣x)2,
(2﹣x)2,
∴y=![]() x2﹣2x+2;
x2﹣2x+2;
(4)当Q与C重合时,E为BC的中点,
即2x=2,
∴x=1,
当Q为BC的中点时,BQ=![]() ,
,
PB=1,
∴AP=3,
∴2x=3,
∴x=![]() ,
,
∴边BC的中点落在正方形DEFQ内部时x的取值范围为:1<x<![]() .
.

 每课必练系列答案
每课必练系列答案 巧学巧练系列答案
巧学巧练系列答案