题目内容
【题目】如图,已知矩形ABCD中,AB=4,AD=m,动点P从点D出发,在边DA上以每秒1个单位的速度向点A运动,连接CP,作点D关于直线PC的对称点E,设点P的运动时间为t(s).
(1)若m=6,求当P,E,B三点在同一直线上时对应的t的值.
(2)已知m满足:在动点P从点D到点A的整个运动过程中,有且只有一个时刻t,使点E到直线BC的距离等于3,求所有这样的m的取值范围.

【答案】(1) ![]() ;(2)
;(2) ![]() ≤m<4
≤m<4![]() .
.
【解析】
试题分析:(1)只要证明△ABD∽△DPC,可得![]() ,由此求出PD即可解决问题;
,由此求出PD即可解决问题;
(2)分两种情形求出AD的值即可解决问题:①如图2中,当点P与A重合时,点E在BC的下方,点E到BC的距离为3.②如图3中,当点P与A重合时,点E在BC的上方,点E到BC的距离为3
试题解析:(1)如图1中,
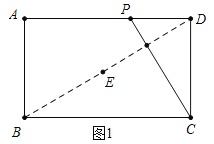
∵四边形ABCD是矩形,
∴∠ADC=∠A=90°,
∴∠DCP+∠CPD=90°,
∵∠CPD+∠ADB=90°,
∴∠ADB=∠PCD,
∵∠A=∠CDP=90°,
∴△ABD∽△DPC,
∴![]() ,
,
∴![]() ,
,
∴PD=![]() ,
,
∴t=![]() s时,B、E、D共线.
s时,B、E、D共线.
(2)如图2中,当点P与A重合时,点E在BC的下方,点E到BC的距离为3.
作EQ⊥BC于Q,EM⊥DC于M.则EQ=3,CE=DC=4
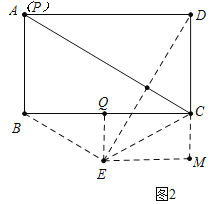
易证四边形EMCQ是矩形,
∴CM=EQ=3,∠M=90°,
∴EM=![]() ,
,
∵∠DAC=∠EDM,∠ADC=∠M,
∴△ADC∽△DME,
![]() ,
,
∴![]() ,
,
∴AD=4![]() ,
,
如图3中,当点P与A重合时,点E在BC的上方,点E到BC的距离为3.
作EQ⊥BC于Q,延长QE交AD于M.则EQ=3,CE=DC=4
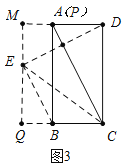
在Rt△ECQ中,QC=DM=![]() ,
,
由△DME∽△CDA,
∴![]() ,
,
∴![]() ,
,
∴AD=![]() ,
,
综上所述,在动点P从点D到点A的整个运动过程中,有且只有一个时刻t,使点E到直线BC的距离等于3,这样的m的取值范围![]() ≤m<4
≤m<4![]() .
.