Question

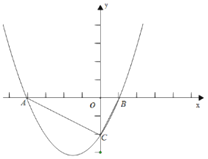
【题目】如图，已知直线经过点和，分别与x轴、y轴交于A、B两点．

(1)求直线的解析式：

(2)若把横、纵坐标均为整数的点称为格点，则图中阴影部分(不包括边界)所含格点的个数有　　　个；

(3)作出点关于直线的对称点，则点的坐标为　　　；

(4)若在直线和轴上分别存在一点使的周长最短，请在图中标出点(不写作法，保留痕迹).

Answer 1

【答案】(1)；(2)10；(3)作图见解析，D(6，2)；(4)作图见解析

【解析】

(1)先利用待定系数法求得直线AB的解析式为；
(2)分别把x=2、3、4、5代入，求出对应的纵坐标，从而得到图中阴影部分(不包括边界)所含格点的坐标；
(3)首先作出点C关于直线AB的对称点D，根据直线AB的解析式可知△OAB是等腰直角三角形，然后根据轴对称的性质即可求出点D的坐标；
(4)作出点C关于直线y轴的对称点E，连接DE交AB于点M，交y轴于点N，则此时△CMN的周长最短．

(1)设直线AB的解析式为，
把(1，5)，(4，2)代入得，，

解得，
∴直线AB的解析式为；
(2)当x=2，y=4；
当x=3，y=3；
当x=4，y=2；
当x=5，y=1．
∴图中阴影部分(不包括边界)所含格点的有：
(1，1)，(1，2)，(1，3)，(1，4)，
(2，1)，(2，2)，(2，3)，
(3，1)，(3，2)，
(4，1)．
一共10个；
故答案为：10；
(3)如图，点D就是所求作的点；

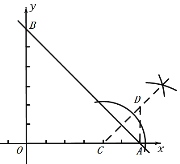
∵直线与轴、y轴交于A、B两点，

令，则；令，则；
∴A点坐标为(6，0)，B点坐标为(0，6)，
∴OA=OB=6，∠OAB=45°．

∵点C关于直线AB的对称点为D，点C(4，0)，
∴AD=AC=2，AB⊥CD，
∴∠DAB=∠CAB=45°，
∴∠DAC=90°，
∴点D的坐标为(6，2)；
(4)如图，点M、N就是所求的点；

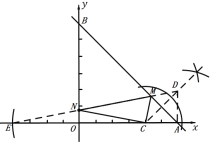
作出点C关于直线y轴的对称点E，连接DE交AB于点M，交y轴于点N，则NC=NE，点E(-4，0)．
又∵点C关于直线AB的对称点为D，
∴CM=DM，
∴△CMN的周长=CM+MN+NC=DM+MN+NE=DE，此时周长最短．