题目内容
【题目】如图，PA为⊙O的切线，A为切点。过A作OP的垂线AB，垂足为点C，交⊙O于点B。延长BO与⊙O交于点D，与PA的延长线交于点E。
（1）求证：PB为⊙O的切线；
（2）试探究线段AD、AB、CP之间的等量关系，并加以证明。
【答案】（1）证明见解析；（2）AB2=2ADPC，证明见解析.
【解析】试题分析：（1）要证PB是⊙O的切线，只要连接OA，再证∠PBO=90°即可；
（2）根据△OCB∽△BCP，可得到BC2=OCPC．再由OC=
AD，BC=
AB，得到结论：AB2=2ADPC．
试题解析：（1）证明：连接OA．∵PA为⊙O的切线，∴∠PAO=90°．
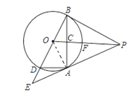
∵OA=OB，OP⊥AB于C，∴BC=CA，PB=PA．
在△PBO和△PAO中，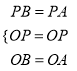 
，∴△PBO≌△PAO，
∴∠PBO=∠PAO=90°，∴PB为⊙O的切线．
（2）AB2=2ADPC．证明如下：
∵∠OBP=∠BCO=90°，∴△OCB∽△BCP，∴
，即BC2=OCPC．
∵OC=
AD，BC=
AB，∴
=
ADPC，∴AB2=2ADPC．
练习册系列答案
相关题目
【题目】刘明上周末买进某只股票2000股，每股38元，下表为本周内每日该股票的涨跌情况（单位：元）
星期 | 一 | 二 | 三 | 四 | 五 | 六 |
每股涨跌 | +2.1 | +1.5 | -2 | -1 | +3.8 | -2.7 |
（1）星期三收盘时，每股是多少元？
（2）本周内最高价是每股多少元？最低每股多少元？
（3）已知买进股票时付了1.5‰的手续费，卖出时需付成交额1.5‰的手续费和1‰的交税，刘明周六收盘前全部卖出股票获利多少？
