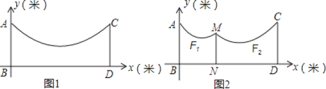Question

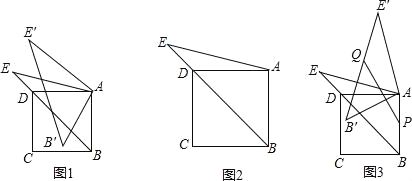
【题目】如图1，等腰中，点分别在腰上，连结，若，则称为该等腰三角形的逆等线．

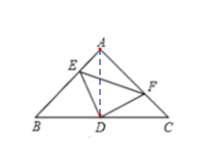
（1）如图1，是等腰的逆等线，若，求逆等线的长；

（2）如图2，若直角的直角顶点恰好为等腰直角底边上的中点，且点分别在上，求证：为等腰的逆等线；

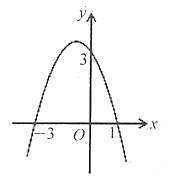
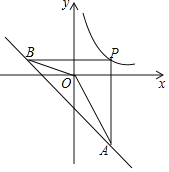
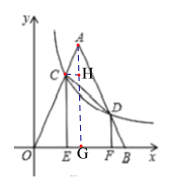
（3）如图3，等腰的顶点与原点重合，底边在轴上，反比例函数的图象交于点，若恰为的逆等线，过点分别作轴于点轴于点，已知，求的长．

Answer 1

【答案】（1）；（2）见解析；（3）．

【解析】

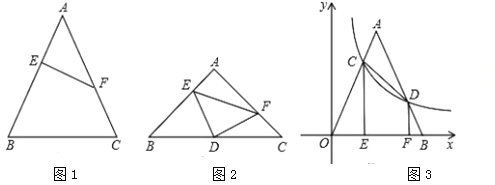
（1）由是等腰的逆等线，得CF=AE=2，根据勾股定理，即可得到答案；

（2）连接AD，根据等腰直角三角形的性质，得AD=DC=BD，∠EAD=∠FCD=45°，AD⊥BC，从而得∠ADE=∠CDF，进而证：ADECDF（ASA），即可得到结论；

（3）设OF=x，则DF=，作AG⊥OB于点G，CH⊥AG于点H，易证△ACH△DBF(AAS)，得EG=CH=BF，AH=DF，进而得EG=x4，由△ACH~△COE，得，列出关于x的方程，即可求解．

（1）∵是等腰的逆等线，

∴CF=AE=2，

∵，

∴AF=5-2=3，

∵，

∴；

（2）连接AD，

∵点为等腰直角底边上的中点，

∴AD=DC=BD，∠EAD=∠FCD=45°，AD⊥BC，

∵∠EDF=90°，

∴∠ADE+∠ADF=∠CDF+∠ADF=90°，

∴∠ADE=∠CDF，

∴ADECDF（ASA），

∴AE=CF，

∴为等腰的逆等线；

（3）设OF=x，则DF=，

作AG⊥OB于点G，CH⊥AG于点H，

∵CD为的逆等线，

∴AC=BD，

∵是等腰三角形，

∴∠ACH=∠AOB=∠DBF，∠AHC=∠AGO=∠DFB=90°，

在△ACH和△DBF中

∵，

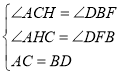∴△ACH△DBF(AAS)，

∴EG=CH=BF，AH=DF，

又∵AO=AB，且AG⊥OB，

∴OG=BG，

∴GF=BGBF=OGEG=OE，

∴EG=x22=x4，

∵△ACH~△COE，

∴，即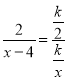：，化简得：x24x4=0，解得：x1=，x2= (舍去)，

∴OF=．