题目内容
【题目】在△OAB中,OA=OB,OA⊥OB.在△OCD中,OC=OD,OC⊥OD.
(1)如图1,若A,O,D三点在同一条直线上,求证:S△AOC=S△BOD;
(2)如图2,若A,O,D三点不在同一条直线上,△OAB和△OCD不重叠.则S△AOC=S△BOD是否仍成立?若成立,请予以证明;若不成立,也请说明理由.
(3)若A,O,D三点不在同一条直线上,△OAB和△OCD有部分重叠,经过画图猜想,请直接写出 S△AOC和S△BOD的大小关系.
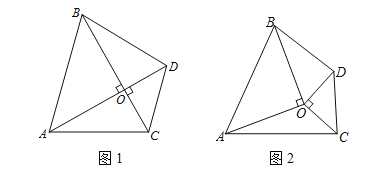
【答案】(1)答案见解析;(2)S△AOC=S△BOD仍成立;(3)S△AOC=S△BOD.
【解析】试题分析:(1)由OA=OB,OC=OD,再结合三角形面积公式即可得到结论;
(2)作DE⊥OB于E,作CF⊥OA交AO的延长线于F.通过证明
△OED≌△OFC,得到DE=CF,再由三角形面积公式即可得到结论;
(3)类似(2)可得结论.
试题解析:解:(1)∵A,O,D三点在一条直线上,OA⊥OB,OC⊥OD,∴∠BOD=∠AOC=90°,∴S△AOC=![]() OAOC,S△BOD=
OAOC,S△BOD=![]() OBOD.
OBOD.
∵OA=OB,OC=OD,∴S△AOC=S△BOD.
(2)S△AOC=S△BOD仍成立.证明如下:
作DE⊥OB于E,作CF⊥OA交AO的延长线于F.
∵∠BOF=∠COD=90°,∴∠BOD=∠COF.
在△OED和△OFC中, 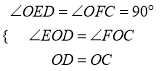 ,
,
∴△OED≌△OFC(AAS),∴DE=CF,∴S△AOC=![]() OACF,S△BOD=
OACF,S△BOD=![]() OBDE,
OBDE,
∴S△AOC=S△BOD.
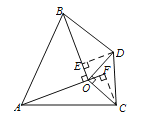
(3)S△AOC=S△BOD.

 各地期末复习特训卷系列答案
各地期末复习特训卷系列答案 小博士期末闯关100分系列答案
小博士期末闯关100分系列答案【题目】小明抛硬币的过程(每枚硬币只有正面朝上和反面朝上两种情况)见下表,阅读并回答问题:
抛掷结果 | 10次 | 50次 | 500次 | 5000次 |
出现正面次数 | 3 | 24 | 258 | 2498 |
出现正面的频率 | 30% | 48% | 51.6% | 49.96% |
(1)从表中可知,当抛完10次时正面出现3次,正面出现的频率为30%,那么,小明抛完10次时,得到 次反面,反面出现的频率是 ;
(2)当他抛完5000次时,反面出现的次数是 ,反面出现的频率是 ;
(3)通过上表我们可以知道,正面出现的频数和反面出现的频数之和等于
,正面出现的频率和反面出现的频率之和等于 .