题目内容
【题目】如图,有一直径是 ![]() 米的圆形铁皮,现从中剪出一个圆周角是90°的最大扇形ABC,则:
米的圆形铁皮,现从中剪出一个圆周角是90°的最大扇形ABC,则: 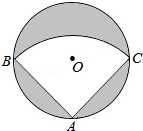
(1)AB的长为米;
(2)用该扇形铁皮围成一个圆锥,所得圆锥的底面圆的半径为米.
【答案】
(1)1
(2)![]()
【解析】解:(1.)∵∠BAC=90°, ∴BC为⊙O的直径,即BC= ![]() ,
,
∴AB= ![]() BC=1;
BC=1;
(2.)设所得圆锥的底面圆的半径为r,
根据题意得2πr= ![]() ,
,
解得r= ![]() .
.
所以答案是:1, ![]() .
.
【考点精析】解答此题的关键在于理解圆周角定理的相关知识,掌握顶点在圆心上的角叫做圆心角;顶点在圆周上,且它的两边分别与圆有另一个交点的角叫做圆周角;一条弧所对的圆周角等于它所对的圆心角的一半,以及对圆锥的相关计算的理解,了解圆锥侧面展开图是一个扇形,这个扇形的半径称为圆锥的母线;圆锥侧面积S=πrl;V圆锥=1/3πR2h..

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目