题目内容
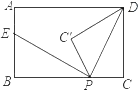
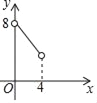
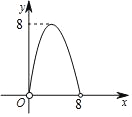
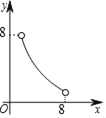
【题目】如图,在平面直角坐标系中,已知![]() ,
,![]() ,
,![]() .
.
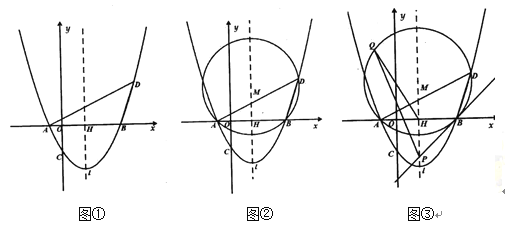
(1)求过点![]() 、
、![]() 、
、![]() 三点的抛物线解析式;
三点的抛物线解析式;
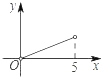
(2)在抛物线上取点![]() ,若点
,若点![]() 的横坐标为10,求点
的横坐标为10,求点![]() 的坐标及
的坐标及![]() 的度数;
的度数;
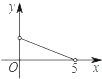
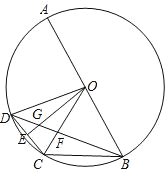
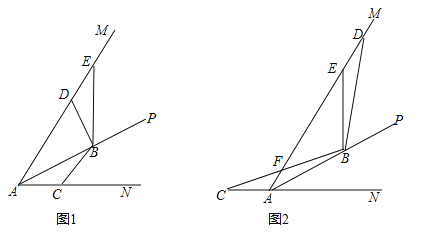
(3)设抛物线对称轴![]() 交
交![]() 轴于点
轴于点![]() ,
,![]() 的外接圆圆心为
的外接圆圆心为![]() (如图②)
(如图②)
①求点![]() 的坐标及⊙
的坐标及⊙![]() 的半径;
的半径;
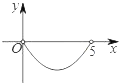
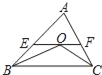
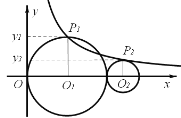
②过点![]() 作⊙
作⊙![]() 的切线交于
的切线交于![]() 于点
于点![]() (如图③),设
(如图③),设![]() 为⊙
为⊙![]() 上一动点,则在点
上一动点,则在点![]() 运动过程中
运动过程中![]() 的值是否变化?若不变,求出其值;若变化,请说明理由.
的值是否变化?若不变,求出其值;若变化,请说明理由.
【答案】(1)![]() ;(2)
;(2)![]() ,
,![]() ;(3)①圆心
;(3)①圆心![]() 的坐标为
的坐标为![]() ,⊙
,⊙![]() 的半径为
的半径为![]() ,②
,②![]() 的值不变,
的值不变, ![]() .
.
【解析】
(1)用待定系数法即可求出过A,B,C三点的抛物线解析式.
(2)先求出D点坐标,再过点![]() 作
作![]() 于点
于点![]() ,过点
,过点![]() 作
作![]() 轴于点
轴于点![]() ,分别在两个直角三角形中求出∠ADB的度数.
,分别在两个直角三角形中求出∠ADB的度数.
(3)①![]() 为等腰直角三角形,圆心
为等腰直角三角形,圆心![]() 在对称轴
在对称轴![]() 上,
上,![]() ,易知点
,易知点![]() 的坐标及⊙
的坐标及⊙![]() 的半径.
的半径.
②连结![]() ,
,![]() ,易得
,易得![]() ,
,![]() ,
,![]() ,再结合
,再结合![]() 即可.
即可.
解:(1)设抛物线为![]() ,
,
将![]() 代入得
代入得![]()
![]() .
.
(2)把![]() 代入
代入![]() ,得
,得![]()
![]() 点
点![]() 的坐标为
的坐标为![]()
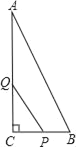
如图①,过点![]() 作
作![]() 于点
于点![]() ,过点
,过点![]() 作
作![]() 轴于点
轴于点![]()
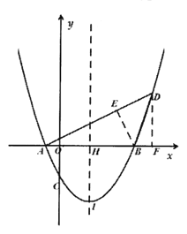
图①
![]() ,
,![]() ,
,![]()
![]()
易得![]() ,
,
求得![]() ,
,![]() ,
,
![]() ,
,
![]()
![]()
(3)①![]() 为等腰直角三角形
为等腰直角三角形
![]() 圆心
圆心![]() 在对称轴
在对称轴![]() 上,
上,![]()
![]() 点
点![]()
![]()
![]() 圆心
圆心![]() 的坐标为
的坐标为![]() ,⊙
,⊙![]() 的半径为
的半径为![]() .
.
②![]() 的值不变,
的值不变,
如图②,连结![]() ,
,![]()
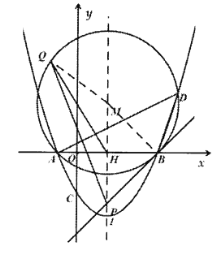
易得![]() ,
,![]() ,
,![]() ,
,
![]() 是⊙
是⊙![]() 的切线
的切线
![]()
![]() ,
,
又![]()
![]()
![]() 的值不变,为
的值不变,为![]()

练习册系列答案
相关题目