题目内容
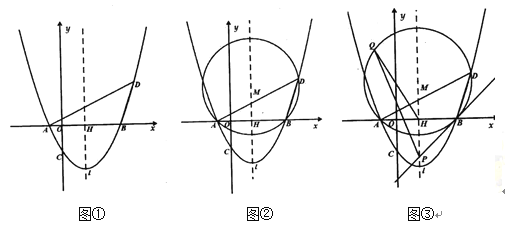
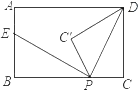
【题目】如图,矩形ABCD中,AB=3,BC=5,点P是BC边上的一个动点(点P不与点B、C重合),现将△PCD沿直线PD折叠,使点C落到点C′处;作∠BPC′的角平分线交AB于点E.设BP=x,BE=y,则下列图象中,能表示y与x的函数关系的图象大致是( )
A. 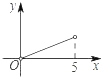 B.
B. 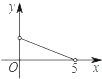 C.
C. 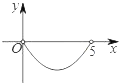 D.
D. 
【答案】D
【解析】
连接DE,根据折叠的性质可得∠CPD=∠C′PD,再根据角平分线的定义可得∠BPE=∠C′PE,然后证明∠DPE=90°,从而得到△DPE是直角三角形,再分别表示出AE、CP的长度,然后利用勾股定理进行列式整理即可得到y与x的函数关系式,根据函数所对应的图象即可得解.
如图,连接DE,
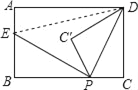
∵△PC′D是△PCD沿PD折叠得到,
∴∠CPD=∠C′PD,
∵PE平分∠BPC′,
∴∠BPE=∠C′PE,
∴∠EPC′+∠DPC′=![]() ×180°=90°,
×180°=90°,
∴△DPE是直角三角形,
∵BP=x,BE=y,AB=3,BC=5,
∴AE=AB﹣BE=3﹣y,CP=BC﹣BP=5﹣x,
在Rt△BEP中,PE2=BP2+BE2=x2+y2,
在Rt△ADE中,DE2=AE2+AD2=(3﹣y)2+52,
在Rt△PCD中,PD2=PC2+CD2=(5﹣x)2+32,
在Rt△PDE中,DE2=PE2+PD2,
则(3﹣y)2+52=x2+y2+(5﹣x)2+32,
整理得,﹣6y=2x2﹣10x,
所以y=﹣![]() x2+
x2+![]() x(0<x<5),
x(0<x<5),
纵观各选项,只有D选项符合.
故选D.

练习册系列答案
相关题目