题目内容
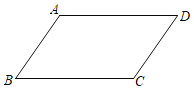
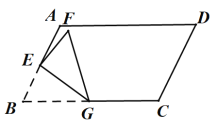
【题目】如图,![]() ,点G为边BC上一点,且
,点G为边BC上一点,且![]() ,点E为AB上一动点,将
,点E为AB上一动点,将![]() 沿
沿![]() 折叠,当点B的对应点F落在平行四边形的边上时,线段
折叠,当点B的对应点F落在平行四边形的边上时,线段![]() 的长为_______.
的长为_______.
【答案】![]()
【解析】
分两种情况:①当F在AB上时,由折叠的性质可知:∠BEG=90°;然后求得∠BGE=30°,最后根据30°所对的边是斜边的一半即可;②当F在AB上时,过A作AH⊥BG.先求出AG、BH的长,然后根据折叠的性质得到FG=BG=2![]() ,∠EFG=60°;再证明四边形AFGH是矩形,得到HG=BG-BH=2
,∠EFG=60°;再证明四边形AFGH是矩形,得到HG=BG-BH=2![]() -2;再根据等角对等边得到AE=AF=2
-2;再根据等角对等边得到AE=AF=2![]() -2,最后根据线段的和差解答即可.
-2,最后根据线段的和差解答即可.
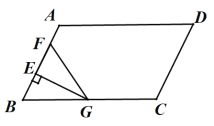
解:如图:当F在AB上时,由折叠的性质可知:∠BEG=90°
∵∠B=60°
∴∠BGE=30°
∵BG=2![]()
∴BE=![]() =
=![]() .
.
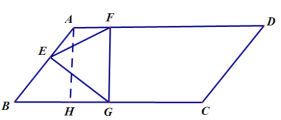
如图:当F在AB上时,过A作AH⊥BG,
∵∠B=60°,AB=4
∴AH=AB·sin∠B=4×![]() =2
=2![]() ,∠BAH=30°
,∠BAH=30°
∴BH=![]() =2
=2
由折叠的性质可得FG=BG=2![]() ,∠EFG=60°,
,∠EFG=60°,
∴AH//FG,即FG⊥AD,∠AFE=30°
∵平行四边形ABCD
∴AD∥BC
∴四边形AFGH是矩形, ∠BAF=180°-∠B=120°
∵HG=BG-BH=2![]() -2
-2
∴AF=HG=2![]() -2,∠AEF=180°-∠EAF-∠AFE=30°
-2,∠AEF=180°-∠EAF-∠AFE=30°
∴∠AEF=∠AFE
∴AE=AF=2![]() -2
-2
∴BE=AB-AE=4-(2![]() -2)=6-2
-2)=6-2![]() .
.
故答案为![]() 或6-2
或6-2![]() .
.

【题目】为了提高学生身体素质,某市中小学开展阳光健步走活动,某数学兴趣小组收集了某校![]() 名学生一天行走的步数并记录如下:
名学生一天行走的步数并记录如下:
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
对这![]() 个数据按组距
个数据按组距![]() 进行分组,并统计整理,绘制了如下尚不完整的统计图表.
进行分组,并统计整理,绘制了如下尚不完整的统计图表.
调查结果统计表:
组别 | 步数分组 | 频数 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
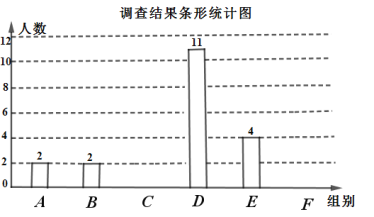
请根据以上信息,解答下列问题:
(1)填空:![]() ,
,![]()
(2)请补全条形统计图.
(3)这![]() 名学生一天行走步数的众数落在 组.
名学生一天行走步数的众数落在 组.
(4)根据科学研究,初中生一天的健步行走应不少于![]() 步,若该校有
步,若该校有![]() 名初中生,请你估计该校一天健步行走不少于
名初中生,请你估计该校一天健步行走不少于![]() 步的学生人数,并根据上述数据,给校方提出合理化的建议(有利于健步行走的)
步的学生人数,并根据上述数据,给校方提出合理化的建议(有利于健步行走的)