��Ŀ����
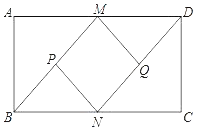
����Ŀ����ͼ1����A��O��B��ͬһֱ���ϣ���AOC=60�㣬��ֱ��AB��һ�ֱ࣬��������DOE��ֱ�Ƕ���O��ʱ����ת����OD��OC�غ�ʱֹͣ�������BOE=����
��1����ͼ1����DO���ӳ���OFƽ�֡�BOC������=______�ȣ�
��2����ͼ2������1����ֱ��������DOE������ʱ����ת����ODλ�ڡ�AOC���ڲ����ҡ�AOD=![]() ��AOC������=__�ȣ�
��AOC������=__�ȣ�
��3��������ֱ��������DOE����ת�����У�����COD+�������Ķ����Ƿ�ı䣿�����ı䣬���������������ı䣬��˵�����ɣ�
���𰸡���1��30 ����2�� 110����3������COD+�������Ķ������䣬������.
��������
��1���ȸ����ڲ��Ƕ���ͽ�ƽ���ߵĶ��������BOF�Ķ������ٸ�����ǵĶ��弴����������Ķ�����
��2�����ݡ�AOD=![]() ��AOC�á�AOD=20�㣬������ǵĶ���������AOE=70�㣬�ٸ��ݲ��ǵĶ��弴����������Ķ�����
��AOC�á�AOD=20�㣬������ǵĶ���������AOE=70�㣬�ٸ��ݲ��ǵĶ��弴����������Ķ�����
��3�������ܽǵ���360��ɵá�COD+����=360��-��DOE-��BOC����DOE���BOC�Ĵ�С���䣬��֪����COD+�������Ķ���������Ϊ150�㣮
�⣺��1����DO���ӳ���OFƽ�֡�BOC����AOC=60�㣬
���BOF=![]() ��BOC=
��BOC=![]() ��180��-��AOC��=
��180��-��AOC��=![]() ��180��-60�㣩=60�㣬
��180��-60�㣩=60�㣬
�֡ߡ�DOE=90�㣬
�����=90��-��BOF=90��-60��=30�㣮
�ʴ�Ϊ��30
��2����ODλ�ڡ�AOC���ڲ����ҡ�AOD=![]() ��AOCʱ����AOD=
��AOCʱ����AOD=![]() ��
��
�֡ߡ�DOE=90�㣬
���AOE=90��-��AOD=90��-20��=70�㣬
�����=180��-��AOE=180��-70��=110�㣮
�ʴ�Ϊ��110
��3������COD+�������Ķ������䣮
�������£�
�ߣ���COD+������+��DOE+��BOC=360�㣬
�ߡ�DOE=90�㣬��BOC=120�㣬
���COD+����=360��-90��-120��=150�㣮
�ࣨ��COD+�������Ķ���������Ϊ150�㣮